- А
- Абсолютно непрерывное
- распределение : 7.2
- совместное распределение : 9.2.2
- Алгебра
: 4.1.1
- тривиальная : 4.1.1
- Атом
: 7.2
- Б
- Бернулли
- закон больших чисел : 12.3
- распределение : 7.4.2
- схема : 6.1
- формула : 6.1
- Берри — Эссеена неравенство
: 13.5
- Биномиальное распределение
: 6.1
| 7.4.3
- дисперсия : 10.5
- математическое ожидание : 10.5
- характеристическая функция : 14.1
- Борелевская
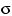 -алгебра : 4.1.3 -алгебра : 4.1.3
- функция : 8.1
- Бюффона задача об игле
: 3.1.2
- Вероятности
- аксиомы : 4.2.2
- свойства : 4.2.2
- В
- Вероятностное пространство
: 4.2.2
- Вероятность
: 4.2.2
- апостериорная : 5.4
- априорная : 5.4
- геометрическая : 3.1
- классическая : 2.2.5
- условная : 5.1
- Вложенные шары
: 4.2.1
- Выбор
- без возвращения : 2.1.2
| 2.1.3
| 2.1.4
- без учёта порядка : 2.1.2
| 2.1.4
| 2.1.6
- с возвращением : 2.1.2
| 2.1.5
| 2.1.6
- с учётом порядка : 2.1.2
| 2.1.3
| 2.1.5
- Вырожденное распределение
: 7.4.1
- дисперсия : 10.5
- математическое ожидание : 10.5
- Г
- Гамма-распределение
: 7.5.4
- характеристическая функция : 14.1
- Гамма-функция Эйлера
: 7.5.4
- Гаусса распределение
: 7.5.3
- Геометрическая вероятность
: 3.1
- Геометрическое распределение
: 6.2
| 7.4.4
- дисперсия : 10.5
- математическое ожидание : 10.5
- Гипергеометрическое распределение
: 2.2.6
| 7.4.6
- дисперсия : 11.4
- математическое ожидание : 11.4
- Д
- Дискретное пространство элементарных исходов
: 2.2.4
- Дискретное распределение
: 7.2
- Дисперсия
: 10.3
- разности : 10.4
- распределения
- Бернулли : 10.5
- биномиального : 10.5
- геометрического : 10.5
- гипергеометрического : 11.4
- Коши : 10.5
- нормального : 10.5
- Парето : 10.5
- показательного : 10.5
- Пуассона : 10.5
- равномерного : 10.5
- стандартного нормального : 10.5
- суммы : 10.4
| 11.1
- суммы
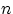 слагаемых : 11.1 слагаемых : 11.1
- Достоверное событие
: 2.2.2
- З
- Задача
- Бюффона об игле : 3.1.2
- о встрече : 3.1.1
- о рассеянной секретарше : 4.2.2
- Закон больших чисел
: 12.3
- Бернулли : 12.3
- Маркова : 12.3
- Хинчина : 12.3
| 14.3
- Чебышёва : 12.3
- И
- Игла Бюффона
: 3.1.2
- Измеримая функция
: 7.1
- Индикатор события
: 12.2
- Интеграл Пуассона
: 7.5.3
- К
- Кантора лестница
: 7.6.4
- Квантильное преобразование
: 8.2.2
- Классическая вероятность
: 2.2.5
- Ковариация
: 11.1
- Конечное множество
: 2.2.4
- Коши распределение
: 7.5.5
- Коэффициент корреляции
: 11.2
- свойства : 11.3
- Л
- Лестница Кантора
: 7.6.4
- М
- Максимума распределение
: 15
- Математическое ожидание
- абсолютно непрерывного распределения : 10.1
- дискретного распределения : 10.1
- постоянной : 10.2
- произведения : 10.2
- распределения
- Бернулли : 10.5
- биномиального : 10.5
- геометрического : 10.5
- гипергеометрического : 11.4
- Коши : 10.5
- нормального : 10.5
- Парето : 10.5
- показательного : 10.5
- Пуассона : 10.5
- равномерного : 10.5
- стандартного нормального : 10.5
- суммы : 10.2
- Мера
: 4.2.1
- вероятностная : 4.2.2
- Лебега : 4.2.1
- нормированная : 4.2.2
- Минимальная
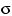 -алгебра
: 4.1.3 -алгебра
: 4.1.3
- Минимума распределение
: 15
- Множество
- всех подмножеств : 4.1.1
- Витали : 3.2
| 8.1
- конечное : 2.2.4
- неизмеримое : 3.2
- пустое : 2.2.2
- счётное : 2.2.4
- Модуль комплексного числа
: 14
- Момент
- первый : 10.1
- порядка
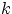 : 10.3 : 10.3
- абсолютный : 10.3
- центральный : 10.3
- абсолютный центральный : 10.3
- факториальный : 10.5
- Муавра — Лапласа теорема
: 13.4
- Н
- Наудачу
: 3.1
- Невозможное событие
: 2.2.2
- Независимость
- испытаний : 6.1
- случайных величин
- в совокупности : 9.5
- попарная : 9.5
- событий : 5.2
- в совокупности : 5.2
- попарная : 5.2
- Неизмеримое множество
: 3.2
| 8.1
- Непрерывность меры
: 4.2.1
- Неравенство
- Берри — Эссеена : 13.5
- Йенсена : 10.3
- Маркова : 12.2
- Чебышёва : 12.2
- обобщённое : 12.2
- Несовместные события
: 2.2.3
- Номер первого успеха
: 6.2
- Нормальное распределение
: 7.5.3
- дисперсия : 10.5
- математическое ожидание : 10.5
- свойства : 7.7
- характеристическая функция : 14.2
- О
- Объединение событий
: 2.2.3
- Определение вероятности
- геометрическое : 3.1
- классическое : 2.2.5
- П
- Парето распределение : 7.5.6
- Пересечение событий
: 2.2.3
- Перестановка
: 2.1.3
- Плотность
- распределения : 7.2
- распределения суммы : 9.6
- совместного распределения : 9.2.2
- Показательное распределение
: 7.5.2
- дисперсия : 10.5
- математическое ожидание : 10.5
- характеристическая функция : 14.1
- Полиномиальное распределение
: 6.3
- Полная группа событий
: 5.3
- Попарно несовместные события
: 2.2.3
- Правило трёх сигм
: 7.7
| 12.2
- Пример Бернштейна : 5.2
- Пространство элементарных исходов
: 2.2.2
- дискретное : 2.2.4
- Противоположное событие
: 2.2.3
- Пуассона
- интеграл : 7.5.3
- приближение : 6.5
- распределение : 6.5
| 7.4.5
- Пустое множество
: 2.2.2
|
- Р
- Распределение
: 2.2.6
- абсолютно непрерывное : 7.2
- Бернулли : 7.4.2
- моменты : 10.5
- характеристическая функция : 14.1
- биномиальное : 6.1
| 7.4.3
- моменты : 10.5
- характеристическая функция : 14.1
- вектора
- абсолютно непрерывное : 9.2.2
- дискретное : 9.2.1
- вектора
- вырожденное : 7.4.1
- моменты : 10.5
- гамма : 7.5.4
- характеристическая функция : 14.1
- Гаусса : 7.5.3
- геометрическое : 6.2
| 7.4.4
- моменты : 10.5
- гипергеометрическое : 2.2.6
| 7.4.6
- моменты : 11.4
- дискретное : 7.2
- Коши : 7.5.5
- моменты : 10.5
- максимума : 15
- маргинальное, или частное : 9.2.1
- минимума : 15
- многомерное нормальное : 9.3.2
- нормальное : 7.5.3
- моменты : 10.5
- свойства : 7.7
- характеристическая функция : 14.2
- Парето : 7.5.6
- моменты : 10.5
- показательное : 7.5.2
- моменты : 10.5
- характеристическая функция : 14.1
- полиномиальное : 6.3
- равномерное : 7.5.1
- моменты : 10.5
- Пуассона : 6.5
| 7.4.5
- моменты : 10.5
- характеристическая функция : 14.1
- равномерное в области : 9.3.1
- корреляция координат : 11.4
- сингулярное : 7.2
- Симпсона : 9.7
- случайной величины : 7.2
- абсолютно непрерывное : 7.2
- дискретное : 7.2
- сингулярное : 7.2
- смешанное : 7.2
- смешанное : 7.2
- совместное : 9.1
- стандартное нормальное : 7.5.3
- моменты : 10.5
- характеристическая функция : 14.1
- числа успехов : 6.1
- экспоненциальное : 7.5.2
- моменты : 10.5
- характеристическая функция : 14.1
- Равномерное распределение
: 7.5.1
- дисперсия : 10.5
- математическое ожидание : 10.5
- Разбиение пространства элементарных исходов
: 5.3
- Размещение
: 2.1.3
- С
- Свойство
- непрерывности меры : 4.2.1
- нестарения
- геометрического распределения : 6.2
- показательного распределения : 7.5.2
- отсутствия последействия
- геометрического распределения : 6.2
- показательного распределения : 7.5.2
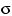 -алгебра
: 4.1.2 -алгебра
: 4.1.2
- борелевская : 4.1.3
- минимальная : 4.1.3
- Сингулярное распределение
: 7.2
- Случайная величина
: 7.1
- Случайные величины
- независимые
- в совокупности : 9.5
- попарно : 9.5
- некоррелированные : 11.3
- отрицательно коррелированные : 11.3
- положительно коррелированные : 11.3
- Смешанное распределение
: 7.2
- Событие
: 2.2.2
| 4.1.1
| 4.1.3
- достоверное : 2.2.2
- невозможное : 2.2.2
- противоположное, или дополнительное : 2.2.3
- События
- вложенные : 2.2.3
- несовместные : 2.2.3
- независимые : 5.2
- попарно : 5.2
- в совокупности : 5.2
- попарно несовместные : 2.2.3
- Сочетание
: 2.1.4
- Среднее значение
: 10.1
- Среднеквадратическое отклонение
: 10.3
- Стандартное нормальное распределение
: 7.5.3
- дисперсия : 10.5
- математическое ожидание : 10.5
- характеристическая функция : 14.1
- Статистическая устойчивость
: 2.2.1
- Схема Бернулли
: 6.1
- Сходимость
- моментов : 12.1
- по вероятности : 12.1
- свойства : 12.1
- по распределению : 13.2
- почти наверное : 12.1
- слабая : 13.2
- свойства : 13.2
- Счётная аддитивность
- вероятности : 4.2.2
- меры : 4.2.1
- Счётное множество
: 2.2.4
- Т
- Таблица
- распределения : 7.2
- совместного распределения : 9.2.1
- Теорема
- закон больших чисел
- Бернулли : 12.3
- Хинчина : 12.3
| 14.3
- Маркова : 12.3
- Чебышёва : 12.3
- Лебега : 7.2
- Леви : 14.2
- Муавра — Лапласа : 13.4
- неравенство Берри — Эссеена : 13.5
- о непрерывном соответствии : 14.2
- о перемножении шансов : 2.1.1
- о вложенных шарах : 4.2.1
- предельная для гипергеометрического распределения : 6.4
- Пуассона : 6.5
- с оценкой точности : 6.5
- умножения вероятностей : 5.1
- центральная предельная : 13.3
| 14.4
- ЦПТ Ляпунова : 13.3
| 14.4
- Тривиальная алгебра
: 4.1.1
- У
- Урновая схема
: 2.1.2
- Условная вероятность
: 5.1
- Устойчивость по суммированию
- биномиального распределения : 9.7
- гамма-распределения : 9.7
- нормального распределения : 9.7
- распределения Пуассона : 9.7
- Ф
- Факториальный момент
: 10.5
- Формула
- Байеса : 5.4
- Бернулли : 6.1
- включения-исключения : 4.2.2
- обратного преобразования Фурье : 14.2
- полной вероятности : 5.3
- свёртки : 9.6
- Эйлера : 14
- Функция
- борелевская : 8.1
- измеримая : 7.1
- по Борелю : 8.1
- распределения : 7.3
- вектора : 9.1
- свойства : 7.6.1
- совместного распределения : 9.1
- характеристическая : 14
- свойства : 14.2
- Х
- Характеристическая функция
: 14
- свойства : 14.2
- Ц
- Центральная предельная теорема
: 13.3
| 14.4
- Ч
- Число
- перестановок : 2.1.3
- размещений : 2.1.3
- сочетаний : 2.1.4
- Э
- Экспоненциальное распределение
: 7.5.2
- дисперсия : 10.5
- математическое ожидание : 10.5
- характеристическая функция : 14.1
- Элементарный исход
: 2.2.2
|
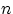 слагаемых : 11.1
слагаемых : 11.1
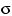 -алгебра
: 4.1.3
-алгебра
: 4.1.3
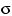 -алгебра
: 4.1.2
-алгебра
: 4.1.2