next up previous contents index
Next:  Формула полной вероятности   Up:  Условная вероятность, независимость   Previous:  Условная вероятность

§ 2. Независимость

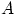
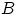
Определение 19. События и называются независимыми, если .
Пример 19.

1. Точка с координатами , бросается наудачу в единичный квадрат со сторонами, параллельными осям координат. Доказать, что для любых события и независимы.

2. Точка с координатами , бросается наудачу в треугольник с вершинами , и . Доказать, что события и зависимы.

1. Решение. Рассмотрим (разобрать остальные случаи). Тогда , , , т.е. события и независимы.

2. Решение. Вычислив соответствующие площади в треугольнике, получим: , , , т.е. события и зависимы.

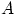
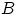
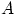
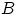
Естественно считать события и независимыми, когда условная вероятность при условии, что произошло, остаётся такой же, как и безусловная. Убедимся, что этим свойством обладают события, независимые согласно определению 19.
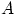
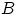
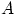
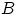
Свойство 4. Пусть . Тогда события и независимы тогда и только тогда, когда . Если , то события и независимы тогда и только тогда, когда .
Упражнение 23. Доказать, пользуясь определением условной вероятности.
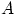
Свойство 5. Пусть события и 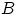несовместны. Тогда независимыми они будут только в том случае, если или .
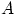
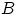
Это свойство (а вы его доказали?) означает, что в невырожденном случае (когда вероятности событий положительны) несовместные события не могут быть независимыми. Зависимость между ними — просто причинно-следственная: если , то , т.е. при выполнении событие не происходит. Это свойство можно сформулировать иначе: в невырожденном случае независимые события просто обязаны пересекаться, т.е. быть совместными.
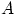
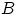
Упражнение 24. Доказать с помощью свойства монотонности вероятности, что событие , вероятность которого равна нулю или единице, не зависит ни от какого события , в том числе и от самого себя.
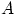
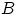
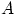
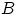
Свойство 6. Если события и независимы, то независимы и события и , и , и .
Доказательство. Так как , и события и несовместны, то . Поэтому

.

Вывести отсюда остальные утверждения.

QED

Если у нас не два, а большее число событий, выполнение только одного равенства вовсе не означает независимости этих событий. Например, при таком равенстве события и вполне могут оказаться зависимыми (привести соответствующий пример). Хотелось бы независимостью нескольких событий считать такое свойство, при котором любые комбинации этих событий оказываются независимыми между собой, например и независимы.
Определение 20. События называются независимыми в совокупности, если для любого и любого набора различных меж собой индексов имеет место равенство:
(6)
Замечание 8. Если события независимы в совокупности, то они попарно независимы, т.е. любые два события независимы. Достаточно в равенстве (6) взять . Обратное, как показывает следующий пример, неверно: из попарной независимости не вытекает независимость в совокупности.
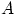
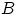
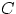
Пример 20.  (пример Бернштейна(1)). Рассмотрим правильный тетраэдр, три грани которого окрашены соответственно в красный, синий, зелёный цвета, а четвёртая грань содержит все три цвета. Событие (соответственно, , ) означает, что выпала грань, содержащая красный (соответственно, синий, зелёный) цвета.

Вероятность каждого из этих событий равна 1/2, так как каждый цвет есть на двух гранях из четырёх. Вероятность пересечения любых двух из них равна 1/4, так как только одна грань из четырёх содержит два цвета. А так как 1/4 = 1/2 · 1/2, то все события попарно независимы.

Но вероятность пересечения всех трёх тоже равна 1/4, а не 1/8, т.е. события не являются независимыми в совокупности.

Заметьте, что равенство (6) выполнено при , но не при .

next up previous contents index
Next:  Формула полной вероятности   Up:  Условная вероятность, независимость   Previous:  Условная вероятность


1Сергей Натанович Бернштейн (5.03.1880 — 26.10.1968) .

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

N.Ch.