



Next: Функция распределения
Up: Случайные величины и их
Previous: Случайные величины
Можно представлять себе распределение случайной величины

как
соответствие между множествами
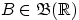
и вероятностями
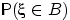
.
Распределения случайных величин суть основные объекты изучения в теории
вероятностей. Мы не будем, как правило, интересоваться тем, из какого множества
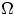 действует функция
действует функция  и каким именно элементарным исходам сопоставляет свои возможные значения.
Нас чаще будет интересовать то, на множестве какой вероятности
эти значения принимаются. Приведём несколько примеров совершенно разных
случайных величин, имеющих одно и то же распределение (одинаково распределённых).
и каким именно элементарным исходам сопоставляет свои возможные значения.
Нас чаще будет интересовать то, на множестве какой вероятности
эти значения принимаются. Приведём несколько примеров совершенно разных
случайных величин, имеющих одно и то же распределение (одинаково распределённых).
Пример.
1. Один раз бросается правильная монета. Пространство
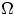 состоит из двух элементарных исходов — герб и решка. В качестве
состоит из двух элементарных исходов — герб и решка. В качестве
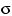 -алгебры рассмотрим
множество всех подмножеств
-алгебры рассмотрим
множество всех подмножеств 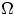 .
Вероятность зададим как в классической схеме.
Зададим две случайные величины
.
Вероятность зададим как в классической схеме.
Зададим две случайные величины  и
и  так:
положим
так:
положим
 =1, если
=1, если 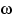 = герб, и
= герб, и  =0, если
=0, если 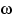 = решка;
= решка;
 =0, если
=0, если 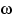 = герб, и
= герб, и  =1, если
=1, если 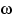 = решка.
= решка.
Очевидно, для любого множества  вероятности принадлежать
вероятности принадлежать 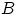 для
для  и
и  одинаковы. Тем не менее ни для одного элементарного
исхода
одинаковы. Тем не менее ни для одного элементарного
исхода 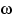 значения
значения  и
и  не совпадают. Т.е.
не совпадают. Т.е.  и
и  одинаково распределены, но не
одинаковы (как функции).
одинаково распределены, но не
одинаковы (как функции).
2.
Точка наудачу бросается на отрезок [0, 1]. В этом случае 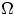 есть отрезок [0, 1] с сигма-алгеброй борелевских подмножеств
есть отрезок [0, 1] с сигма-алгеброй борелевских подмножеств 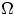 и мерой Лебега. Предлагаю читателю убедиться, что две
совершенно разные функции:
и мерой Лебега. Предлагаю читателю убедиться, что две
совершенно разные функции: 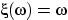 и
и  (расстояния до упавшей точки от левого и от правого концов
отрезка соответственно) обладают одинаковыми вероятностями
принимать значения внутри любых борелевских множеств
(расстояния до упавшей точки от левого и от правого концов
отрезка соответственно) обладают одинаковыми вероятностями
принимать значения внутри любых борелевских множеств 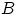 (вероятности, равные мере Лебега пересечения множеств
(вероятности, равные мере Лебега пересечения множеств 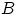 и [0, 1]). Таким образом, эти случайные величины
снова одинаково распределены, но не одинаковы: их значения
совпадают лишь при одном элементарном исходе
и [0, 1]). Таким образом, эти случайные величины
снова одинаково распределены, но не одинаковы: их значения
совпадают лишь при одном элементарном исходе 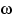 = 0.5 (нарисовать графики функций
= 0.5 (нарисовать графики функций
 и
и  ).
).
3. На том же самом отрезке [0, 1] построим две функции:
 =0 при всех
=0 при всех 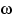 ;
;  =0 при всех
=0 при всех 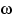 , кроме
, кроме 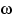 = 0.5, а в точке
= 0.5, а в точке 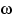 = 0.5 положим
= 0.5 положим  = —17.
= —17.
Поскольку мера Лебега точки (она же — вероятность)
равна нулю, распределения величин  и
и  одинаковы. Теперь
одинаковы. Теперь  и
и  снова не совпадают как функции, но отличаются их
значения лишь на множестве нулевой вероятности (только в точке 0.5). В этом случае говорят,
что
снова не совпадают как функции, но отличаются их
значения лишь на множестве нулевой вероятности (только в точке 0.5). В этом случае говорят,
что  и
и  совпадают «почти наверное»:
совпадают «почти наверное»:
 .
.
Опишем различные типы распределений случайных величин.
Вся вероятностная масса может быть сосредоточена в нескольких точках прямой,
может быть «размазана» по некоторому интервалу или по всей прямой.
В зависимости от типа множества, на котором сосредоточена вся единичная вероятностная масса,
распределения делят на дискретные, абсолютно непрерывные, сингулярные и их смеси.
Определение 29.
Cлучайная величина

имеет
дискретное
распределение, если существует конечный или счётный набор чисел

такой, что

Итак, случайная величина

имеет дискретное распределение,
если она принимает не более чем счётное число значений.
Значения эти иначе называют
атомами:

имеет атом в точке
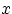
, если

.
Если случайная величина  имеет дискретное распределение,
то для любого
имеет дискретное распределение,
то для любого 

Дискретное распределение удобно задавать следующей
таблицей, в которой  :
:

Определение 30.
Cлучайная величина

имеет
абсолютно непрерывное
распределение, если существует неотрицательная функция
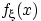
такая, что
для любого борелевского множества
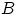
имеет место равенство:

Функцию 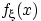 называют плотностью распределения случайной величины
называют плотностью распределения случайной величины  .
.
Теорема 17.
Плотность распределения обладает свойствами:
(f1) 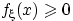 для любого
для любого 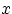 ;
(f2)
;
(f2)  .
.
Доказательство.
(f1) выполнено по определению плотности,
(f2) также следует из определения:

QED
Эти два свойства полностью характеризуют класс плотностей:
Теорема 18.
Если функция
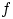
обладает свойствами
(f1) и
(f2),
то существует вероятностное пространство и случайная величина

на нём, для которой
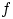
является плотностью распределения.
Доказательство.
Пусть
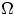
есть область, заключенная между осью абсцисс
и графиком функции
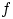
.
Площадь области
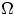
равна единице по свойству
(f2).
Пусть

— множество
борелевских подмножеств 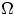
, а
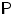
—
мера Лебега (площадь) на множествах из

.
И пусть случайная величина

есть абсцисса точки, наудачу брошенной
в эту область.

Тогда для любого
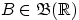
выполнено:
 | (10) |
Здесь область  есть криволинейная трапеция под графиком плотности, с основанием
есть криволинейная трапеция под графиком плотности, с основанием 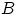 .
По определению, равенство (10) означает, что функция
.
По определению, равенство (10) означает, что функция 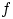 является плотностью распределения
случайной величины
является плотностью распределения
случайной величины  .
.
QED
Свойство 7.
Если случайная величина

имеет абсолютно непрерывное
распределение, то

для любого
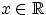
.
Доказательство. Доказательство сразу следует из
определения 30
и
замечания 11,
так как интеграл по области интегрирования,
состоящей из одной точки, равен нулю.
QED
Можно выделить ещё один особый класс
распределений, сосредоточенных, в отличие от абсолютно непрерывных распределений, на множестве нулевой
меры Лебега, но не имеющих, в отличие от дискретных, атома ни в одной точке этого множества.
Определение 31.
Говорят, что случайная величина

имеет
сингулярное
распределение, если существует борелевское множество
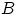
с нулевой лебеговой мерой

такое,
что

, но при этом

для любой точки

.
Можно отметить следующее свойство сингулярных распределений. Множество
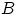
, на котором сосредоточено всё распределение, не может состоять из конечного или счётного числа точек. Действительно,
если
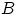 конечно или счётно
конечно или счётно,
то 
, где суммирование ведётся
по всем

. Последняя сумма равна нулю как сумма счётного числа нулей,
что противоречит предположению

.
Таким образом, любое сингулярное распределение сосредоточено на несчётном множестве
с нулевой мерой Лебега. Примером такого множества может служить канторовское совершенное
множество, а примером такого распределения — лестница Кантора (выяснить, что это такое!).
Наконец, распределение может быть выпуклой линейной комбинацией
дискретного, абсолютно непрерывного и сингулярного распределений.
Определение 32.
Говорят, что случайная величина

имеет
смешанное
распределение, если найдутся такие случайные величины
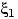
,
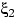
и

— с дискретным, абсолютно
непрерывным и сингулярным распределениями соответственно (или такие три распределения), и
числа

,

, что для любого
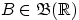
имеет место равенство:

По заданным на одном вероятностном пространстве случайным величинам
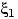
,
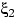
,

и числам

можно построить случайную
величину со смешанным распределением так: пусть

— случайная
величина с дискретным распределением на том же вероятностном пространстве такая,
что

для

, и при любом
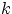
и любом
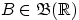
события

и

независимы.
Построим случайную величину  так:
так:
 , если
, если  , где
, где  .
Её распределение найдём по формуле полной вероятности:
.
Её распределение найдём по формуле полной вероятности:

В силу независимости событий под знаком каждой из вероятностей,

Никаких других видов распределений, кроме перечисленных
выше, не существует (доказано Лебегом

).




Next: Функция распределения
Up: Случайные величины и их
Previous: Случайные величины
N.Ch.
![]() действует функция
действует функция ![]() и каким именно элементарным исходам сопоставляет свои возможные значения.
Нас чаще будет интересовать то, на множестве какой вероятности
эти значения принимаются. Приведём несколько примеров совершенно разных
случайных величин, имеющих одно и то же распределение (одинаково распределённых).
и каким именно элементарным исходам сопоставляет свои возможные значения.
Нас чаще будет интересовать то, на множестве какой вероятности
эти значения принимаются. Приведём несколько примеров совершенно разных
случайных величин, имеющих одно и то же распределение (одинаково распределённых).


 .
.


