Свойства функций распределения

Next: Свойства нормального распределения Up: Случайные величины и их Previous: Примеры абсолютно непрерывных распределений

§ 6. Свойства функций распределения

Общие свойства функций распределения.

Функцией распределения случайной величины

мы назвали функцию

. Основные свойства этой функции заключены в теореме:

Теорема 20. Любая функция распределения обладает следующими свойствами:

(F1): она не убывает: если , то ;
(F2): cуществуют пределы и ;
(F3): она в любой точке непрерывна слева:

Доказательство свойства (F1). Для любых чисел

событие

влечёт событие

, т.е.

. Но вероятность — монотонная функция событий, поэтому

QED

Для доказательства остальных свойств нам понадобится свойство непрерывности вероятностной меры.

Доказательство свойства (F2). Заметим сначала, что существование пределов в свойствах (F2), (F3) вытекает из монотонности и ограниченности функции

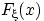
. Остается лишь доказать равенства

, и .

Для этого в каждом случае достаточно найти предел по какой-нибудь подпоследовательности , так как существование предела влечёт совпадение всех частичных пределов.

Докажем, что при . Рассмотрим вложенную убывающую последовательность событий :

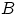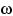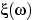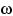Пересечение всех этих событий состоит из тех и только тех , для которых меньше любого вещественного числа. Но для любого элементарного исхода значение 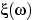вещественно, и не может быть меньше всех вещественных чисел. Иначе говоря, пересечение событий не содержит элементарных исходов, т.е. . По свойству непрерывности меры, при .

Точно так же докажем остальные свойства.

Покажем, что при , т.е. . Обозначим через событие . События вложены:

а пересечение 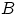этих событий снова пусто — оно означает, что больше любого вещественного числа. По свойству непрерывности меры, при .

Доказательство свойства (F3). Достаточно доказать, что

при

. Иначе говоря, доказать сходимость к нулю следующей разности:

Упражнение 30. Обозначьте событие

через

, и попробуйте снова воспользоваться свойством непрерывности меры.

QED

Следующая теорема говорит о том, что три доказанных свойства полностью описывают класс функций распределения. То, что любая функция распределения ими обладает, мы с вами доказали, а теорема утверждает, что любая функция с такими свойствами есть функция распределения.

Теорема 21. Если функция

удовлетворяет свойствам (F1)—(F3), то

есть функция распределения некоторой случайной величины

, т.е. найдётся вероятностное пространство

и случайная величина

на нём такая, что

Эту теорему мы доказывать не станем. Хотя её можно попробовать доказать конструктивно — предъявив то вероятностное пространство (проще всего отрезок

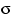
-алгеброй борелевских множеств и мерой Лебега) и ту случайную величину, о существовании которых идёт речь.

Упражнение 31. Непременно попробуйте сделать это! Например, можно попробовать, не подойдёт ли

Помимо отмеченных в теореме 20, функции распределения обладают следующими свойствами:

(F4)

В любой точке

разница

равна

или, иначе говоря, .

Упражнение 32. Докажите сами (так же, как мы доказывали (F2) и (F3)).

Заметим, что разница

между пределом при стремлении к

справа и значением в точке

есть величина скачка функции распределения. Эта величина равна нулю, если функция распределения непрерывна (справа) в точке

. Слева функция распределения непрерывна всегда.

Замечание 13. Очень часто функцией распределения называют

. Эта функция отличается от определённой выше лишь тем, что она непрерывна справа, а не слева. Соответственно, вероятность

для неё равна величине скачка слева, а не справа.

(F5)

Для любой случайной величины

имеет место равенство:

(13)

Если же функция распределения 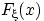непрерывна в точках 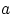и , то

Доказательство. Докажем только равенство (13). Все остальные равенства следуют из него и свойства (F4).

Заметим, что , и первые два события несовместны. Поэтому или , что и требовалось доказать.

QED

Функция распределения дискретного распределения.

Мы видели, как выглядят функции распределения некоторых дискретных распределений. Согласно определению дискретного распределения, его функция распределения может быть найдена по таблице распределения так:

Из свойств (F4) и (F5) получаем следующее свойство.

Свойство 8. Случайная величина

имеет дискретное распределение тогда и только тогда, когда функция распределения

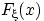
— ступенчатая функция. При этом значения

суть точки

скачков

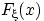
, и

— величины скачков.

Упражнение 33. Доказать, что любая функция распределения имеет не более чем счётное число точек разрыва (или «скачков»). Сколько скачков величиной более 1/2 может иметь функция распределения? Не больше одного или не больше двух? А скачков величиной более 1/3? Более 1/4?

Свойства абсолютно непрерывного распределения.

Пусть случайная величина

имеет абсолюлютно непрерывное распределение с плотностью

. Тогда функция распределения в любой точке

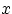
может быть найдена по плотности распределения так:

(14)

Поскольку функция распределения однозначно определяет распределение случайной величины (эту фразу стоит как следует обдумать!), можно считать возможность представить функцию распределения интегралом (14) от неотрицательной функции определением абсолютно непрерывного распределения.

(f3): Если случайная величина имеет абсолютно непрерывное распределение, то её функция распределения всюду непрерывна.

Этот факт следует из свойства 7 и из (F4). Заметим, что (f3) есть также следствие представления (14) и непрерывности интеграла как функции верхнего предела.

(f4): Если случайная величина имеет абсолютно непрерывное распределение, то её функция распределения дифференцируема почти всюду, и

Замечание 14. Термин «почти всюду» означает «для всех

, кроме (возможно)

из некоторого множества нулевой меры Лебега».

Заметим, что любая функция распределения дифференцируема почти всюду. Например, функции распределения равномерного распределения и распределения Бернулли дифференцируемы всюду, кроме двух точек. Но у равномерного распределения плотность существует, а у распределения Бернулли — нет. Поэтому возможность дифференцировать функцию распределения никакого отношения к существованию плотности не имеет. Даже если мы дополнительно потребуем непрерывности функции распределения, этого не будет достаточно для абсолютной непрерывности распределения. Например, далее мы увидим, что функция распределения сингулярного распределения непрерывна и дифференцируема почти всюду, однако плотности у этого распределения нет, так как производная функции распределения почти всюду равна нулю.

Опираясь на свойства (f4) и (14), можно сформулировать такой критерий абсолютной непрерывности распределения: распределение с функцией распределения 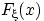абсолютно непрерывно, если при всех 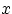имеет место равенство:

Из определения абсолютно непрерывного распределения и свойства 7 сразу следует свойство:

(f5): Если случайная величина имеет абсолютно непрерывное распределение, то для любых имеют место равенства:

Функция распределения сингулярного распределения.

Для полноты картины посмотрим, какие свойства имеет функция распределения сингулярного распределения. Согласно определению 31, случайная величина

с сингулярным распределением принимает с единичной вероятностью лишь значения из некоторого борелевского множества

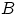
с нулевой лебеговой мерой. Поэтому

. Но согласно равенству (13), если

, то

, т.е. расти функция распределения может лишь в точках множества

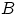
. На всём остальном множестве

функция распределения имеет нулевую производную (в точках, где эта производная существует, т.е. почти всюду). Тем не менее,

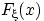
всюду непрерывна, поскольку

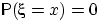
для любой точки

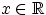
Примером такой функции распределения служит лестница Кантора:

Функция распределения смешанного распределения.

Функция распределения смешанного распределения есть линейная комбинация функций распределения дискретного, абсолютно непрерывного и сингулярного распределений. Если смешивать только дискретное и абсолютно непрерывное распределения, то функция распределения будет иметь разрывы в точках значений дискретного распределения и участки непрерывного роста, приращение функции на которых восстанавливается по её производной.

N.Ch.