Формула Байеса

Теорема 9 (формула Байеса⁽¹⁾). Пусть

— полная группа событий, и

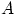
— некоторое событие, вероятность которого положительна. Тогда условная вероятность того, что имело место событие

, если в результате эксперимента наблюдалось событие

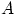
, может быть вычислена по формуле:

Пример 22. Вернёмся к примеру 21. Изделие выбирается наудачу из всей произведённой продукции. Рассмотрим три гипотезы:

. Вероятности этих событий даны:

Пусть . Даны также условные вероятности , , .

Убедитесь, что полученные нами в примере 21 вероятности совпадают с вероятностями, вычисленными по формуле полной вероятности и формуле Байеса.

Пример 23. Два стрелка подбрасывают монетку и выбирают, кто из них стреляет по мишени (одной пулей). Первый стрелок попадает по мишени с вероятностью 1, второй стрелок — с вероятностью 0,00001. Можно сделать два предположения об эксперименте:

. Априорные (a'priori — «до опыта») вероятности этих гипотез одинаковы:

Рассмотрим событие . Известно, что

Поэтому вероятность пуле попасть в мишень

Предположим, что событие 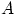произошло. Какова теперь апостериорная (a'posteriori — «после опыта») вероятность каждой из гипотез ? Очевидно, что первая из этих гипотез много вероятнее второй (а именно, в раз). Действительно,

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

§ 4. Формула Байеса