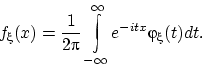
Ни одна из формул обратного преобразования Фурье нам не понадобится.
![]()
QED
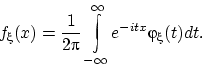
Ни одна из формул обратного преобразования Фурье нам не понадобится.
![]()
![]()
![]()
![]()
Видим, что характеристическая функция суммы есть характеристическая
функция нормального распределения с параметрами
![]() и
и ![]() . Следовательно,
. Следовательно, ![]() по свойству (Ф2).
по свойству (Ф2).
QED
Для независимых случайных величин с распределениями Пуассона ![]() и
и ![]() характеристическая функция суммы
характеристическая функция суммы
![]()
равна характеристической функции распределения Пуассона ![]() .
.
Для независимых случайных величин с биномиальными распределениями
![]() и
и ![]() характеристическая функция суммы
характеристическая функция суммы
![]()
равна характеристической функции биномиального
распределения с параметрами ![]() и
и ![]() .
.
Для ![]() независимых (в совокупности) случайных величин с показательным распределением
независимых (в совокупности) случайных величин с показательным распределением ![]() характеристическая функция суммы
характеристическая функция суммы
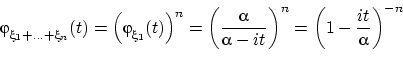
равна характеристической функции гамма-распределения ![]() .
.
QED
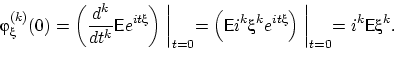
![]()
Доказать по определению, что все моменты нечётных порядков стандартного нормального распределения существуют и равны нулю.
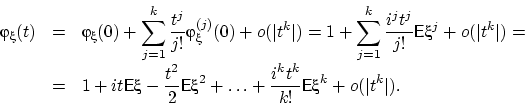
Осталось воспользоваться теоремой о непрерывном соответствии и доказать ЗБЧ в форме Хинчина и ЦПТ.
1Brook Taylor (18.08.1685 — 29.12.1731, England)
2Paul Pierre Lévy (15.09.1886 — 15.12.1971, France)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.