![]() при
при ![]() .
.
Поэтому в определении 53 часто говорят и пишут так:
![]() слабо сходится к распределению
слабо сходится к распределению ![]() , т.е.
, т.е. ![]() , либо даже так:
распределения
, либо даже так:
распределения ![]() слабо сходятся к распределению
слабо сходятся к распределению
![]() :
: ![]() .
.
Следующее свойство уточняет отношения между сходимостями.
Докажем (2): слабая сходимость к постояннной влечёт сходимость по вероятности. Пусть
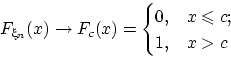
при любом ![]() , являющемся точкой непрерывности предельной функции
, являющемся точкой непрерывности предельной функции
![]() ,
т.е. при всех
,
т.е. при всех ![]() .
.
Возьмём произвольное ![]() и докажем, что
и докажем, что ![]() .
Раскроем модуль:
.
Раскроем модуль:
![]()
![]()
поскольку в точках
![]() и
и ![]() функция
функция ![]() непрерывна, и, следовательно, имеет место сходимость
последовательностей:
непрерывна, и, следовательно, имеет место сходимость
последовательностей: ![]() к
к ![]() и
и
![]() к
к ![]() .
.
Осталось заметить, что ![]() не бывает больше 1, так что по свойству предела зажатой последовательности
не бывает больше 1, так что по свойству предела зажатой последовательности
![]() .
.
QED
Заметим вначале, что если ![]() , то
, то ![]() и
и ![]() (доказать!).
Поэтому достаточно доказать первое утверждение свойства 21 при
(доказать!).
Поэтому достаточно доказать первое утверждение свойства 21 при ![]() ,
а второе утверждение — при
,
а второе утверждение — при ![]() .
.
Рассмотрим второе утверждение, оставив первое любознательному читателю.
Пусть ![]() и
и ![]() .
Докажем, что тогда
.
Докажем, что тогда ![]() .
.
Пусть ![]() — точка непрерывности функции распределения
— точка непрерывности функции распределения
![]() . Требуется доказать, что имеет место
сходимость
. Требуется доказать, что имеет место
сходимость ![]() .
Зафиксируем достаточно маленькое
.
Зафиксируем достаточно маленькое ![]() такое,
что
такое,
что ![]() непрерывна в точках
непрерывна в точках ![]() .
Воспользуемся тем, что события
.
Воспользуемся тем, что события ![]() и
и
![]() образуют полную группу:
образуют полную группу:
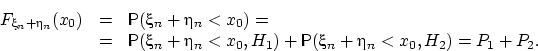
Оценим ![]() сверху и снизу. Для
сверху и снизу. Для ![]() имеем:
имеем:
![]()
и последняя вероятность может быть выбором ![]() сделана сколь угодно малой. Для
сделана сколь угодно малой. Для ![]() , с одной стороны,
, с одной стороны,
![]()
Неравенство следует из очевидного соображения:
если ![]() и
и ![]() , то, тем более,
, то, тем более, ![]() .
.
С другой стороны,
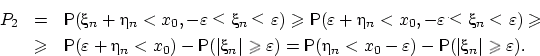
Здесь первое неравенство объясняется включением
![]()
которое получилось заменой в событии ![]() числа
числа ![]() на меньшую величину
на меньшую величину ![]() .
Второе неравенство следует из свойств:
.
Второе неравенство следует из свойств:
![]()
Мы получили оценки снизу и сверху для ![]() , т.е. для
, т.е. для ![]() :
:
![]()
или
![]()
Устремляя ![]() к бесконечности, и вспоминая, что
к бесконечности, и вспоминая, что ![]() — точки непрерывности функции распределения
— точки непрерывности функции распределения ![]() , получим
, получим
![]()
И поскольку эти неравенства верны для любого достаточно малого ![]() такого, что функция распределения
такого, что функция распределения ![]() непрерывна в точках
непрерывна в точках ![]() (множество точек разрыва у любой функции распределения
не более чем счётно, и таких
(множество точек разрыва у любой функции распределения
не более чем счётно, и таких ![]() можно найти сколько угодно в любой окрестности нуля), а
можно найти сколько угодно в любой окрестности нуля), а ![]() — точка непрерывности функции
— точка непрерывности функции ![]() , то, устремив
, то, устремив ![]() к нулю, получим, что нижний и верхний пределы
к нулю, получим, что нижний и верхний пределы
![]() при
при ![]() совпадают и равны
совпадают и равны ![]() .
.
QED
Представим ![]() в виде суммы
в виде суммы ![]() . Здесь
последовательность
. Здесь
последовательность ![]() по вероятности стремится к нулю, а «последовательность»
по вероятности стремится к нулю, а «последовательность»
![]() слабо сходится к
слабо сходится к ![]() . Поэтому их сумма слабо сходится к
. Поэтому их сумма слабо сходится к ![]() .
.
QED
Если ![]() , то утверждение теоремы сразу следует из свойства 21.
Действительно, из
, то утверждение теоремы сразу следует из свойства 21.
Действительно, из ![]() следует, что
следует, что ![]() . К тому же
. К тому же
![]() . Тогда утверждение (2) свойства 21 позволяет заключить,
что
. Тогда утверждение (2) свойства 21 позволяет заключить,
что ![]() . Функция распределения
. Функция распределения
![]() отличается от
отличается от ![]() лишь сдвигом и
тоже непрерывна всюду, поэтому имеет место сходимость функций распределения
в любой точке. В частности, в точке
лишь сдвигом и
тоже непрерывна всюду, поэтому имеет место сходимость функций распределения
в любой точке. В частности, в точке ![]() = 0 имеет место сходимость при
= 0 имеет место сходимость при
![]()
![]()
Пусть теперь ![]() . Нужно доказать, что
. Нужно доказать, что
![]() .
.
По определению, ![]() с ростом
с ростом ![]() , если
для всякого
, если
для всякого ![]() найдётся номер
найдётся номер ![]() такой, что для всех
такой, что для всех ![]() выполнено
неравенство:
выполнено
неравенство: ![]() . В силу монотонности функций распределения,
. В силу монотонности функций распределения,
![]() . В точке —
. В точке —![]() , как и в любой иной точке,
имеет место сходимость функций распределения
, как и в любой иной точке,
имеет место сходимость функций распределения ![]() . Выбором
. Выбором ![]() величина
величина ![]() может быть сделана сколь угодно близкой к нулю.
Тем самым верхний предел последовательности
может быть сделана сколь угодно близкой к нулю.
Тем самым верхний предел последовательности ![]() оказывается
зажат между нулём и сколь угодно малой величиной, т.е. равняется нулю.
оказывается
зажат между нулём и сколь угодно малой величиной, т.е. равняется нулю.
Случай ![]() проверяется аналогично.
проверяется аналогично.
QED
N.Ch.