Описание
распределения набором вероятностей
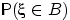
не очень удобно: слишком много
существует борелевских множеств. Мы описали
дискретные распределения таблицей
распределения,
абсолютно непрерывные — плотностью распределения.
Попробуем поискать какой-нибудь универсальный способ описать любое возможное распределение.
Можно поставить вопрос иначе: распределение есть набор вероятностей попадания в любые борелевские множества на прямой.
Нельзя ли обойтись знанием вероятностей попадания в какой-нибудь меньший набор множеств на прямой? Борелевская 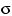 -алгебра
-алгебра 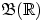 порождается интервалами (равно как и лучами
порождается интервалами (равно как и лучами 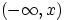 ),
поэтому можно ограничиться только вероятностями попадания в такие лучи для всех
),
поэтому можно ограничиться только вероятностями попадания в такие лучи для всех 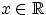 .
А уже с их помощью можно будет определить и вероятность попасть в любое
борелевское множество.
.
А уже с их помощью можно будет определить и вероятность попасть в любое
борелевское множество.
Определение 33.
Функцией распределения
случайной величины

называется функция
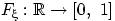
, при каждом
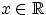
равная вероятности
случайной величине

принимать значения, меньшие
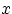
:
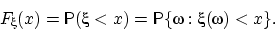
Перечислим основные дискретные и абсолютно непрерывные распределения и найдём их
функции распределения.
![]() -алгебра
-алгебра ![]() порождается интервалами (равно как и лучами
порождается интервалами (равно как и лучами ![]() ),
поэтому можно ограничиться только вероятностями попадания в такие лучи для всех
),
поэтому можно ограничиться только вероятностями попадания в такие лучи для всех ![]() .
А уже с их помощью можно будет определить и вероятность попасть в любое
борелевское множество.
.
А уже с их помощью можно будет определить и вероятность попасть в любое
борелевское множество.