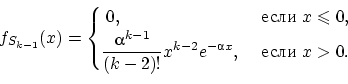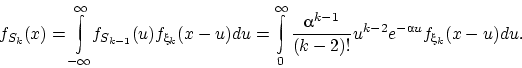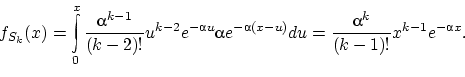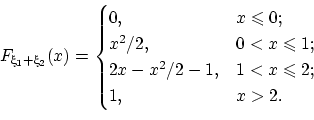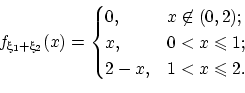Пример 30.
Пусть
независимые случайные величины

и

имеют
стандартное
нормальное распределение. Докажем, что их сумма имеет нормальное распределение
с параметрами
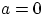
и
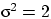
.
По формуле свёртки, плотность суммы равна
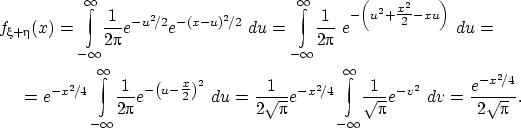
Последний интеграл равен единице, поскольку под интегралом стоит плотность
нормального распределения с параметрами 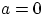 и
и 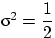 .
.
Итак, мы получили, что плотность суммы есть плотность нормального
распределения с параметрами 0 и 2.
Если сумма двух независимых случайных величин из одного и того же
распределения (возможно, с разными параметрами)
имеет такое же распределение, говорят, что это распределение
устойчиво относительно суммирования.
В следующих утверждениях, доказать которые предлагается читателю,
перечислены практически все устойчивые распределения.
Все эти утверждения мы докажем позднее, используя аппарат
характеристических функций, хотя при некотором терпении
можно попробовать доказать их и напрямую,
как в примере
30.
Показательное распределение не устойчиво по суммированию,
однако оно является частным случаем гамма-распределения,
которое уже устойчиво относительно суммирования.
Доказательство.
Докажем утверждение по индукции. При
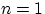
оно верно в силу равенства
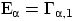
.
Пусть утверждение леммы справедливо для
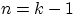
. Докажем, что оно верно
и для
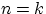
.
По предположению индукции
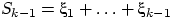
имеет распределение
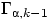
,
т.е. плотность распределения величины
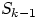
равна
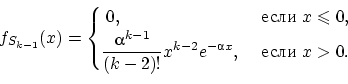
Тогда по формуле свёртки плотность суммы
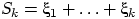 равна
равна
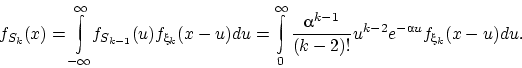
Так как 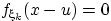 при
при 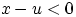 , т.е. при
, т.е. при 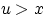 ,
то плотность под интегралом отлична от нуля, только если переменная
интегрирования изменяется в пределах
,
то плотность под интегралом отлична от нуля, только если переменная
интегрирования изменяется в пределах 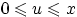 при
при 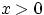 .
При
.
При 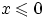 подынтегральная функция, а вместе с ней и плотность
подынтегральная функция, а вместе с ней и плотность 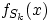 , равна нулю. При
, равна нулю. При 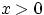 имеем:
имеем:
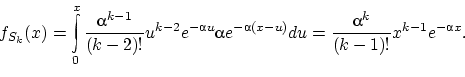
Поэтому  , что и требовалось доказать.
, что и требовалось доказать.
QED
Пример 31.
Равномерное распределение не является устойчивым относительно суммирования.
Найдём функцию и плотность распределения суммы двух независимых случайных
величин с одинаковым равномерным на отрезке [0, 1] распределением, но не
по формуле свёртки, а используя
геометрическую вероятность.
Пусть 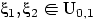 — независимые случайные величины.
Пару
— независимые случайные величины.
Пару  можно считать координатой точки, брошенной наудачу
в единичный квадрат.
Тогда
можно считать координатой точки, брошенной наудачу
в единичный квадрат.
Тогда 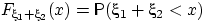 равна площади
области внутри квадрата под прямой
равна площади
области внутри квадрата под прямой 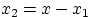 . Эта область
— заштрихованные треугольник при
. Эта область
— заштрихованные треугольник при 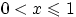 , и пятиугольник при
, и пятиугольник при 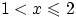 .
Окончательно получаем:
.
Окончательно получаем:
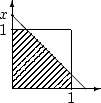
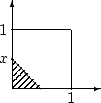
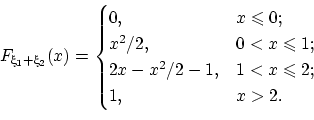
Плотность распределения суммы равна
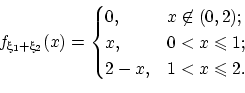
Это — плотность так называемого «треугольного» распределения Симпсона.
Мы видим, что равномерное распределение не обладает устойчивостью относительно суммирования.
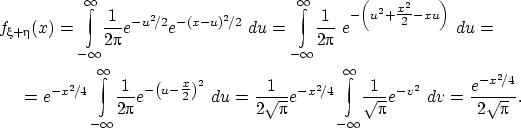
![]() и
и ![]() .
.