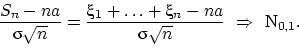
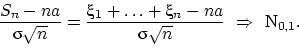
Характеристическая функция величины ![]() равна
равна
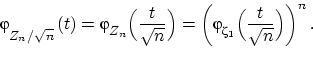 | (27) |
Характеристическую функцию случайной величины ![]() можно разложить в ряд Тейлора,
в коэффициентах которого использовать известные моменты
можно разложить в ряд Тейлора,
в коэффициентах которого использовать известные моменты
![]() ,
, ![]() .
Получим
.
Получим
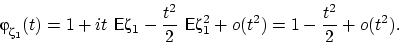
Подставим это разложение, взятое в точке ![]() , в равенство (27)
и устремим
, в равенство (27)
и устремим ![]() к бесконечности. Ещё раз воспользуемся замечательным
пределом.
к бесконечности. Ещё раз воспользуемся замечательным
пределом.
![]()
В пределе получили характеристическую функцию стандартного нормального распределения. По теореме о непрерывном соответствии можно сделать вывод о слабой сходимости
![]()
QED
N.Ch.