В этом разделе, который никогда не будет прочитан на лекциях,
поскольку эта тема подробно разбирается на практических занятиях,
мы поговорим о максимуме и минимуме из
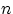
случайных величин.
Вдумчивый читатель уже догадался, что ничего общего с клубом «Максимин»
ЭФ НГУ эта тема не имеет. Нам необходимо уметь обращаться
с минимумом и максимумом из нескольких случайных величин хотя бы потому, что
при изучении математической статистики мы не раз о них вспомним.
Пусть случайные величины 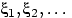 независимы в совокупности и одинаково
распределены,
независимы в совокупности и одинаково
распределены, 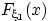 — их общая функция распределения.
— их общая функция распределения.
Упражнение N.
Доказать, что вероятность максимуму из первых
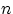
независимых и одинаково распределённых случайных величин,
имеющих абсолютно непрерывное распределение, равняться первой из них, равно как
и любой другой, есть
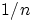
:
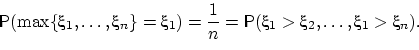
Для доказательства воспользоваться соображениями симметрии, разбив
пространство 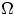 на несколько равновероятных событий
вида
на несколько равновероятных событий
вида 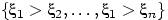 и несколько событий нулевой вероятности, включающих возможные равенства.
Вспомнить, с какой вероятностью две (или больше) из
и несколько событий нулевой вероятности, включающих возможные равенства.
Вспомнить, с какой вероятностью две (или больше) из 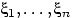 совпадают
(нарисовать событие
совпадают
(нарисовать событие 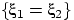 на плоскости).
на плоскости).
Доказательство.
Найдём функцию распределения
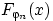
. Максимум из
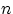
величин меньше
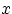
тогда и только тогда, когда каждая из этих величин меньше
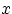
.
Поэтому событие
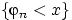
равносильно пересечению
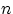
независимых событий
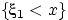
, ...,
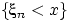
,
имеющих одну и ту же вероятность
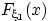
:
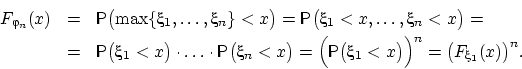
Найдём функцию распределения 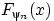 . Минимум из
. Минимум из 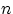 величин не меньше
величин не меньше 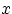 тогда и только тогда, когда каждая из этих величин
не меньше
тогда и только тогда, когда каждая из этих величин
не меньше 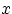 :
:
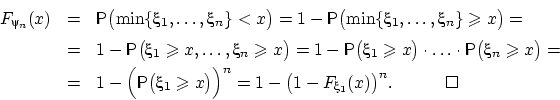
Update: раньше мне не приходило в голову, что "знатоки" из интернета не в состоянии вычленить из
готового рассуждения для минимума независимых и одинаково распределённых случайных величин "формулу" для функции
распределения минимума независимых велчиин с разными распределениями... Оказывается, не могут. Специально для них:
ПОСЛЕДНЮЮ СТРОЧКУ ИГНОРИРУЕМ, И ПОЛУЧАЕМ НУЖНУЮ ФОРМУЛУ!
О, святая дева Мария...
QED
Пример N.
Пусть случайные величины
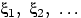
независимы в совокупности и имеют
равномерное распределение на отрезке [0, 1]. Докажем, что
последовательность случайных величин
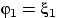
,
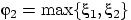
,
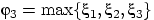
, ...
сходится по вероятности к правому концу отрезка — к единице.
Можно произнести это утверждение так:
«максимум из первых 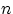 случайных величин с ростом
случайных величин с ростом 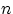 сходится к единице по вероятности».
сходится к единице по вероятности».
Есть как минимум два способа доказательства.
- Способ 1. По определению.
-
Зафиксируем произвольное число
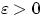 . Заметим, что
. Заметим, что 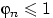 , поскольку это максимум из случайных величин,
принимающих значения на отрезке [0, 1] п.н. Поэтому
, поскольку это максимум из случайных величин,
принимающих значения на отрезке [0, 1] п.н. Поэтому
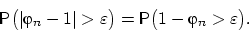
Для того, чтобы установить сходимость последней вероятности к нулю,
можно её либо найти, либо оценить с помощью неравенства Маркова. Сделаем и то, и другое.
(А) Найдём эту вероятность.
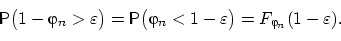
Для равномерного распределения на отрезке [0, 1]
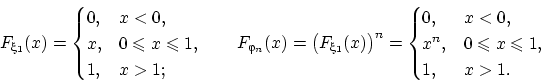
А если ещё заметить, что 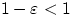 , то
, то
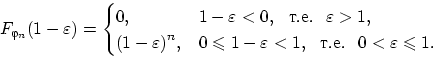
Видно, что 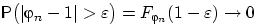 при
при 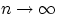 .
.
(Б) Оценим вероятность сверху.
Поскольку 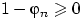 п.н. и
п.н. и 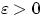 , то по неравенству Маркова
, то по неравенству Маркова
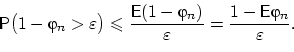 | (28) |
Найдём плотность распределения 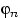 и математическое ожидание
и математическое ожидание
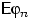 :
:
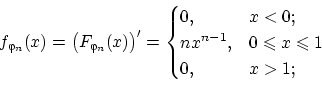
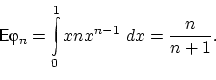
Подставляя математическое ожидание в неравенство (28),
получим
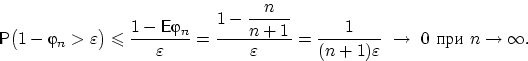
- Способ 2. Используем связь со слабой сходимостью.
-
Сходимость по вероятности к постоянной
равносильна слабой сходимости (свойство 20). Докажем,
что
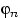 слабо сходится к единице. Требуется доказать,
что функция распределения
слабо сходится к единице. Требуется доказать,
что функция распределения 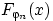 сходится к
сходится к 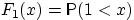 для любого
для любого 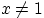 (почему кроме 1?).
(почему кроме 1?).
При любом 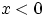 имеем:
имеем: 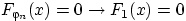 при
при 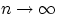 .
При любом
.
При любом 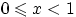 имеем:
имеем: 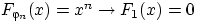 при
при 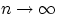 .
При любом
.
При любом 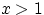 имеем:
имеем: 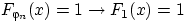 .
И только при
.
И только при 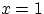 сходимости нет:
сходимости нет: 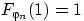 , тогда как
, тогда как
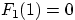 . Но сходимости в точке
. Но сходимости в точке 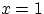 и не требуется — в этой точке
предельная функция распределения терпит разрыв:
и не требуется — в этой точке
предельная функция распределения терпит разрыв:
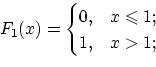
Таким образом, 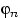 слабо сходится к единице, и, следовательно,
сходится к ней же по вероятности.
слабо сходится к единице, и, следовательно,
сходится к ней же по вероятности.
Упражнение N+1.
Доказать (способами
(1А),
(1Б) и
(2), что, в условиях примера
(N), последовательность
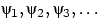 сходится по вероятности
сходится по вероятности к нулю (мы будем говорить
«минимум из первых
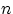
случайных величин с ростом
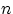
сходится к нулю
по вероятности»).
Красивых задач, связанных с максимумом и минимумом, слишком много.
Предлагаю вам решить, например, следующие:
![]() независимы в совокупности и одинаково
распределены,
независимы в совокупности и одинаково
распределены, ![]() — их общая функция распределения.
— их общая функция распределения.![]() независимы в совокупности и одинаково
распределены,
независимы в совокупности и одинаково
распределены, ![]() — их общая функция распределения.
— их общая функция распределения.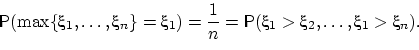
![]() на несколько равновероятных событий
вида
на несколько равновероятных событий
вида ![]() и несколько событий нулевой вероятности, включающих возможные равенства.
Вспомнить, с какой вероятностью две (или больше) из
и несколько событий нулевой вероятности, включающих возможные равенства.
Вспомнить, с какой вероятностью две (или больше) из ![]() совпадают
(нарисовать событие
совпадают
(нарисовать событие ![]() на плоскости).
на плоскости).
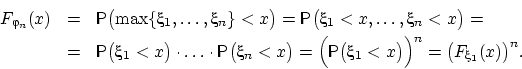
![]() . Минимум из
. Минимум из ![]() величин не меньше
величин не меньше ![]() тогда и только тогда, когда каждая из этих величин
не меньше
тогда и только тогда, когда каждая из этих величин
не меньше ![]() :
:
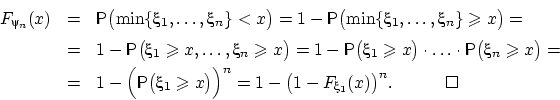
![]() случайных величин с ростом
случайных величин с ростом ![]() сходится к единице по вероятности».
сходится к единице по вероятности».
![]()
![]()
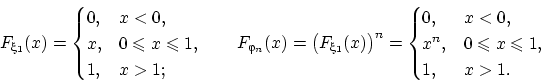
![]() , то
, то
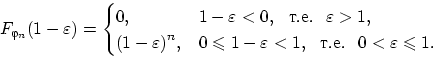
![]() при
при ![]() .
.![]() п.н. и
п.н. и ![]() , то по неравенству Маркова
, то по неравенству Маркова
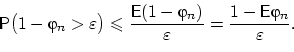
![]() и математическое ожидание
и математическое ожидание
![]() :
:
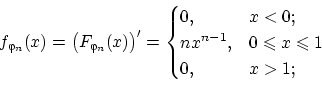
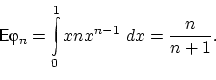
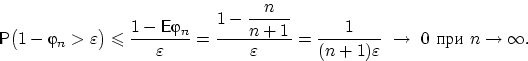
![]() имеем:
имеем: ![]() при
при ![]() .
При любом
.
При любом ![]() имеем:
имеем: ![]() при
при ![]() .
При любом
.
При любом ![]() имеем:
имеем: ![]() .
И только при
.
И только при ![]() сходимости нет:
сходимости нет: ![]() , тогда как
, тогда как
![]() . Но сходимости в точке
. Но сходимости в точке ![]() и не требуется — в этой точке
предельная функция распределения терпит разрыв:
и не требуется — в этой точке
предельная функция распределения терпит разрыв:
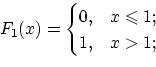
![]() слабо сходится к единице, и, следовательно,
сходится к ней же по вероятности.
слабо сходится к единице, и, следовательно,
сходится к ней же по вероятности.