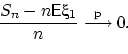
Если при делении на ![]() мы получили в пределе нуль (в смысле некоторой,
всё равно какой, сходимости), резонно задать себе вопрос:
а не слишком ли на большую величину мы поделили? Нельзя ли поделить
на что-нибудь, растущее к бесконечности медленнее, чем
мы получили в пределе нуль (в смысле некоторой,
всё равно какой, сходимости), резонно задать себе вопрос:
а не слишком ли на большую величину мы поделили? Нельзя ли поделить
на что-нибудь, растущее к бесконечности медленнее, чем ![]() , чтобы получить в пределе не нуль (и не бесконечность, само собой)?
, чтобы получить в пределе не нуль (и не бесконечность, само собой)?
Можно поставить этот вопрос по-другому. Вот последовательность, стремящаяся (как-то) к нулю. Можно ли её домножить на что-либо растущее, чтобы «погасить» это стремление к нулю? Получив, тем самым, что-нибудь конечное и отличное от нуля в пределе?
Оказывается, что уже последовательность случайных величин
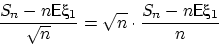
не сходится к нулю. Распределение членов этой последовательности становится всё более похожим на нормальное распределение! Можно считать, что такая последовательность сходится к случайной величине, имеющей нормальное распределение, но сходится никак не по вероятности, а только в смысле сходимости распределений, или «слабой сходимости».