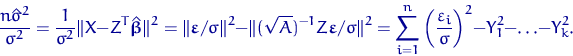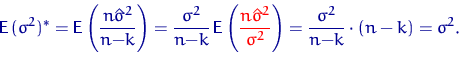


Next: Добавления
Up: Исследование статистической зависимости
Previous: Нормальное уравнение
Отметим несколько свойств, которые, возможно, нам понадобятся в дальнейшем.
- 1.
- Разница
 и
и 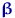 равна
равна 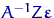 :
:
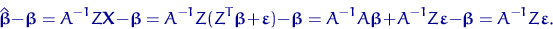
- 2.
- Если
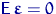 , то
, то 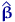 — несмещенная оценка для
— несмещенная оценка для 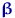 :
:
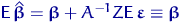 .
.
Пусть выполнены предположения 1 и 2 :
Предположение 2.
Вектор ошибок 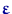 состоит из
независимых случайных величин с нормальным распределением
состоит из
независимых случайных величин с нормальным распределением 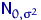 с одной и той же дисперсией.
с одной и той же дисперсией.
Напоминание 3.
Для произвольного случайного вектора
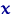
, координаты которого имеют вторые моменты, матрица ковариаций
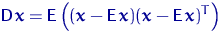
— это матрица, чей
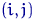
-й элемент равен
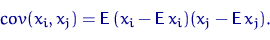
В частности, 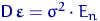 , где
, где  — единичная
— единичная
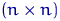 -матрица.
-матрица.
- 3.
- Матрица ковариаций вектора
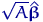 равна
равна  :
:

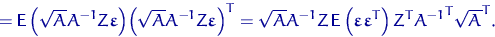
И так как 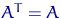 ,
,  , то
, то
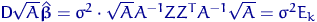 .
.
Свойство 3 означает, что координаты вектора
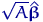 некоррелированы.
Сформулируем дальнейшее следствие этого свойства первым пунктом
следующей теоремы.
С утверждениями второго и третьего пунктов читатель встретится в следующем
семестре многократно.
некоррелированы.
Сформулируем дальнейшее следствие этого свойства первым пунктом
следующей теоремы.
С утверждениями второго и третьего пунктов читатель встретится в следующем
семестре многократно.
Доказательство теоремы 13
- 1.
- Вектор
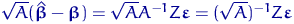 есть линейное преобразование нормального вектора
есть линейное преобразование нормального вектора 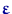 и поэтому имеет нормальное совместное распределение.
По свойству 3,
матрица ковариаций этого вектора есть
и поэтому имеет нормальное совместное распределение.
По свойству 3,
матрица ковариаций этого вектора есть  , поэтому матрица ковариаций нормированного вектора
, поэтому матрица ковариаций нормированного вектора
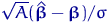 есть просто
есть просто 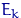 , а математическое ожидание равно нулю по свойству 2.
Напомним, что координаты многомерного нормального вектора независимы
тогда и только тогда, когда они некоррелированы — см. теорему 14.
Первое утверждение теоремы доказано.
, а математическое ожидание равно нулю по свойству 2.
Напомним, что координаты многомерного нормального вектора независимы
тогда и только тогда, когда они некоррелированы — см. теорему 14.
Первое утверждение теоремы доказано.
- 2.
- По построению ОМНК, вектор
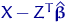 ортогонален любому вектору
вида
ортогонален любому вектору
вида 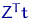 .
В частности, он ортогонален вектору
.
В частности, он ортогонален вектору 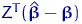 . По теореме Пифагора, для треугольника с такими катетами сумма квадратов их длин
равна квадрату длины гипотенузы:
. По теореме Пифагора, для треугольника с такими катетами сумма квадратов их длин
равна квадрату длины гипотенузы:

Поэтому
 | (35) |
Но квадрат нормы 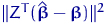 равен
квадрату нормы
равен
квадрату нормы 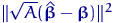 :
:
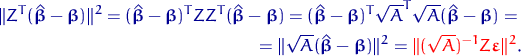
Осталось заметить, что строки  -матрицы
-матрицы
 ортогональны:
ортогональны:
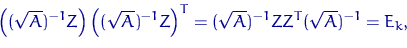
поэтому 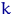 её строк можно дополнить до некоторой ортогональной
её строк можно дополнить до некоторой ортогональной
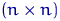 -матрицы
-матрицы 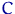 .
Первые
.
Первые 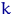 координат
координат 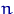 -мерного вектора
-мерного вектора 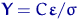 совпадают с вектором
совпадают с вектором 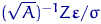 .
В результате из (35) получим
.
В результате из (35) получим
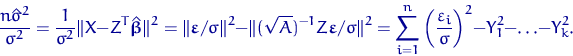 | (36) |
Не забудьте, что вектор 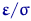 имеет
имеет 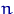 -мерное
стандартное нормальное распределение. Тогда вся
разность (35) по лемме Фишера
имеет распределение
-мерное
стандартное нормальное распределение. Тогда вся
разность (35) по лемме Фишера
имеет распределение 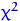 с
с  степенями свободы и не зависит от вычитаемого,
т.е. от случайного вектора
степенями свободы и не зависит от вычитаемого,
т.е. от случайного вектора 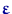 (и от
(и от 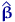 тоже, поскольку
тоже, поскольку 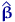 есть функция
есть функция 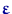 ).
).
- 3.
- Напомним, что
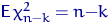 . Отсюда и из второго утверждения
теоремы получим
. Отсюда и из второго утверждения
теоремы получим
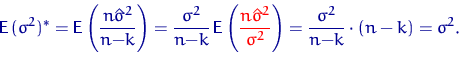
Q.D.E.
N.I.Chernova
9 сентября 2002
![]()
![]()
![]() состоит из
независимых случайных величин с нормальным распределением
состоит из
независимых случайных величин с нормальным распределением ![]() с одной и той же дисперсией.
с одной и той же дисперсией. ![]()
![]() , где
, где ![]() — единичная
— единичная
![]() -матрица.
-матрица.![]()
![]()
![]() ,
, ![]() , то
, то
![]() .
. ![]() некоррелированы.
Сформулируем дальнейшее следствие этого свойства первым пунктом
следующей теоремы.
С утверждениями второго и третьего пунктов читатель встретится в следующем
семестре многократно.
некоррелированы.
Сформулируем дальнейшее следствие этого свойства первым пунктом
следующей теоремы.
С утверждениями второго и третьего пунктов читатель встретится в следующем
семестре многократно. ![]()
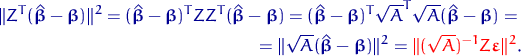
![]() -матрицы
-матрицы
![]() ортогональны:
ортогональны:
![]()
![]() её строк можно дополнить до некоторой ортогональной
её строк можно дополнить до некоторой ортогональной
![]() -матрицы
-матрицы ![]() .
Первые
.
Первые ![]() координат
координат ![]() -мерного вектора
-мерного вектора ![]() совпадают с вектором
совпадают с вектором ![]() .
В результате из (35) получим
.
В результате из (35) получим