next up previous index
Next:  Свойства ОМНК   Up:  Исследование статистической зависимости   Previous:  Общая модель линейной регрессии

9.6.   Метод наименьших квадратов. Нормальное уравнение

Предположение 1.    Матрица $Z$ имеет ранг $k$, т.е. все $k$ ее строк линейно независимы.


Лемма 4.

Предположение 1 означает, что матрица $A=Z{\cdot}Z^T$ положительно определена.

Напоминание 1.    Матрица $A(k\times k)$ положительно определена, если ${\mathbf t}^T A {\mathbf t} \geqslant 0$ для любого ${\mathbf t}= (t_1,\ldots,t_k)$, причем ${\mathbf t}^T A {\mathbf t} = 0$, если и только если ${\mathbf t}=\pmb 0$.

Напоминание 2.    Квадрат нормы вектора ${\mathbf u}$ равен  $\lVert {\mathbf u} \rVert^2={\mathbf u}^T {\mathbf u} = \sum u_i^2 \geqslant 0$. Норма равна нулю, если и только если ${\mathbf u}=\pmb 0$.

Доказательство леммы 4.

Благодаря напоминанию 2,

\begin{displaymath} {\mathbf t}^T A {\mathbf t} = {\mathbf t}^T Z{\cdot}Z^T {\ma... ...^T {\mathbf t}~) = \lVert Z^T {\mathbf t} \rVert^2 \geqslant 0,\end{displaymath}

причем $\lVert Z^T {\mathbf t} \rVert = 0$, если и только если $Z^T {\mathbf t} = \pmb 0$. Но «ранг $Z$ равен $k$» как раз и означает, по определению, что $Z^T {\mathbf t} = \pmb 0$ тогда и только тогда, когда ${\mathbf t}=\pmb 0$.

Q.D.E.


Скоро нам пригодится корень из матрицы $A$, существование которого гарантирует

Лемма 5.

Положительная определенность и симметричность матрицы $A$ влекут существование вещественной симметричной матрицы $\sqrt{A}$ такой, что $\sqrt{A}\sqrt{A}=A$.

Действительно,    матрица $A$ симметрична, поскольку $A=Z Z^T$ и $A^T=A$. Существование(*) матрицы $\sqrt{A}$ с нужными свойствами следует из возможности привести $A$ ортогональными преобразованиями $A=Q^TDQ$ к диагональному виду с положительными, в силу положительной определенности, собственными значениями $A$ на диагонали $D$. Тогда $\sqrt{A}=Q^T\sqrt{D}Q$.

Q.D.E.


Найдем ОМНК $\hat{\text{\boldmath\ensuremath \beta}}$ для вектора $\text{\boldmath\ensuremath \beta}$, доставляющий минимум функции $S(\text{\boldmath\ensuremath \beta})$, равной

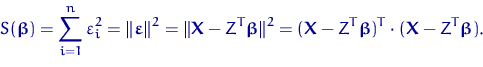
\begin{displaymath} S(\text{\boldmath\ensuremath \beta})=\sum_{i=1}^n \varepsilo... ...eta})^T\cdot({\mathbf X}-Z^T\text{\boldmath\ensuremath \beta}).\end{displaymath}

Вместо того, чтобы искать точку экстремума функции $S(\text{\boldmath\ensuremath \beta})$ дифференцированием по $\beta_i$, заметим следующее. Величина $S(\text{\boldmath\ensuremath \beta})$ есть квадрат расстояния от точки ${\mathbf X}\in{\textrm{\upshape I\kern-0.20em R}}^n$ до точки $Z^T\text{\boldmath\ensuremath \beta}$ — одной из точек линейного подпространства (гиперплоскости) в ${\textrm{\upshape I\kern-0.20em R}}^n$ с координатами вида $Z^T{\mathbf t}$, где ${\mathbf t}\in{\textrm{\upshape I\kern-0.20em R}}^k$. Минимальное расстояние $S(\hat{\text{\boldmath\ensuremath \beta}})$ мы получим, когда вектор ${\mathbf X}-Z^T\hat{\text{\boldmath\ensuremath \beta}}$ будет ортогонален всем векторам этого подпространства, т.е. когда для любого ${\mathbf t}\in{\textrm{\upshape I\kern-0.20em R}}^k$ скалярное произведение векторов $Z^T{\mathbf t}$ и ${\mathbf X}-Z^T\hat{\text{\boldmath\ensuremath \beta}}$ обратится в ноль. Запишем это скалярное произведение в матричном виде

\begin{displaymath} \left(Z^T{\mathbf t},{\mathbf X}-\hat{\text{\boldmath\ensure... ...mathbf X}-ZZ^T\hat{\text{\boldmath\ensuremath \beta}}\right)=0.\end{displaymath}

Подставляя в качестве ${\mathbf t}$ базисные вектора в ${\textrm{\upshape I\kern-0.20em R}}^k$ вида $(0,\ldots,0,1,0,\ldots,0)$, сразу же получим, что все координаты вектора $Z{\mathbf X}-ZZ^T\hat{\text{\boldmath\ensuremath \beta}}$ равны нулю. Итак, оценка метода наименьших квадратов $\hat{\text{\boldmath\ensuremath \beta}}$ есть любое решение уравнения

\begin{equation} ZZ^T\hat{\text{\boldmath\ensuremath \beta}}=Z{\mathbf X} \quad ... ...или } \quad A\hat{\text{\boldmath\ensuremath \beta}}=Z{\mathbf X}.\end{equation}(32)

По лемме 4, уравнение (32) имеет единственное решение

\begin{equation} \hat{\text{\boldmath\ensuremath \beta}}=A^{-1}Z{\mathbf X}\end{equation}(33)

в том и только в том случае, когда матрица $Z(k\times n)$ имеет полный ранг $k$, где $k\leqslant n$. Уравнение (32) называется нормальным уравнением.

В предположении, что вектор ошибок $\text{\boldmath\ensuremath \varepsilon}$ состоит из независимых случайных величин с нормальным распределением ${\mathsf N}_{0,\sigma^2}$ с одной и той же дисперсией, ОМНК совпадает с оценкой максимального правдоподобия, а ОМП для $\sigma^2$, согласно (31), равна

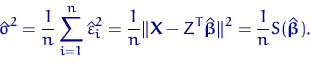\begin{equation} {\hat\sigma}^2=\dfrac{1}{n} \sum_{i=1}^n {\hat\varepsilon}_i^2=... ...}\rVert^2=\dfrac{1}{n} S(\hat{\text{\boldmath\ensuremath \beta}}).\end{equation}(34)


N.I.Chernova
9 сентября 2002

(*) См., например, А.И.Мальцев «Основы линейной алгебры», раздел «Унитарные и евклидовы пространства», параграф «Унитарные и симметрические преобразования», теорема 7.