Пусть ![]() — выборка из
— выборка из ![]() (набор независимых и одинаково распределенных величин).
Пусть
(набор независимых и одинаково распределенных величин).
Пусть ![]() — ортогональная матрица
— ортогональная матрица ![]() , т.е.
, т.е.
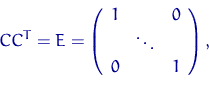
и ![]() — вектор с координатами
— вектор с координатами
![]() .
.
Какое распределение имеют координаты вектора ![]() ? Зависимы ли они?
Чтобы ответить на этот вопрос, выясним, как изменится плотность распределения
вектора после умножения его на произвольную невырожденную матрицу.
? Зависимы ли они?
Чтобы ответить на этот вопрос, выясним, как изменится плотность распределения
вектора после умножения его на произвольную невырожденную матрицу.
![]()
Поверим, без доказательства, аналогичному утверждению в многомерном случае. Те, кто знаком с заменой переменных в многомерном интеграле и не боится термина «якобиан», могут доказать его самостоятельно.
Пусть случайный вектор ![]() имеет плотность распределения
имеет плотность распределения ![]() ,
и
,
и ![]() — невырожденная матрица. Тогда вектор
— невырожденная матрица. Тогда вектор
![]() имеет плотность распределения
имеет плотность распределения
| (16) |
Докажем самое удивительное свойство нормального распределения.
Пусть вектор ![]() состоит из независимых случайных величин со стандартным
нормальным распределением,
состоит из независимых случайных величин со стандартным
нормальным распределением, ![]() — ортогональная матрица, и
— ортогональная матрица, и
![]() . Тогда и координаты вектора
. Тогда и координаты вектора ![]() независимы и имеют
стандартное нормальное распределение.
независимы и имеют
стандартное нормальное распределение.
Доказательство. Запишем плотность совместного распределения координат вектора ![]() .
В силу независимости это есть произведение плотностей координат вектора
(то же самое, что функция правдоподобия):
.
В силу независимости это есть произведение плотностей координат вектора
(то же самое, что функция правдоподобия):
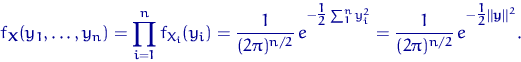
Здесь для произвольного вектора ![]() квадрат нормы
квадрат нормы ![]() есть
есть
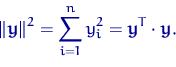
Пользуясь (16), вычислим плотность распределения вектора
![]() . Матрица
. Матрица ![]() ортогональна,
поэтому
ортогональна,
поэтому ![]() и
и ![]() .
.
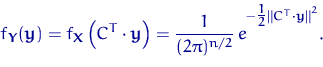
Но умножение на ортогональную матрицу не меняет норму вектора. Действительно,
| (17) |
Окончательно имеем
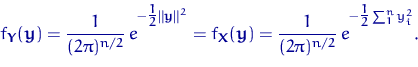
Итак, вектор ![]() распределен так же, как и вектор
распределен так же, как и вектор ![]() ,
т.е. состоит из независимых случайных величин со стандартным
нормальным распределением.
,
т.е. состоит из независимых случайных величин со стандартным
нормальным распределением.
Q.D.E.
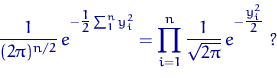
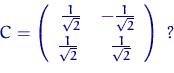
Пусть вектор ![]() состоит из независимых случайных величин со стандартным
нормальным распределением,
состоит из независимых случайных величин со стандартным
нормальным распределением, ![]() — ортогональная матрица, и
— ортогональная матрица, и
![]() . Тогда для любого
. Тогда для любого ![]()
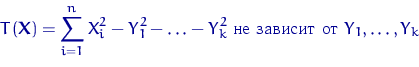
Доказательство. Как мы видели в (17), нормы векторов ![]() и
и ![]() совпадают:
совпадают:
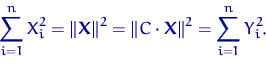
Поэтому
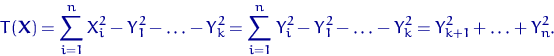
Случайные величины ![]() ,
, ![]() ,
, ![]() по свойству 9 независимы и
имеют стандартное нормальное распределение, поэтому
по свойству 9 независимы и
имеют стандартное нормальное распределение, поэтому
![]() имеет распределение
имеет распределение ![]() и не зависит от
и не зависит от ![]() .
.
Q.D.E.
Второй и третий пункты следующего утверждения выглядят неправдоподобно, особенно если вспомнить обозначения:
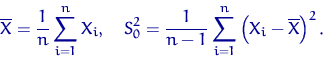
Если
![]() ,
, ![]() ,
, ![]() независимы и имеют
нормальное распределение
независимы и имеют
нормальное распределение ![]() , то
, то
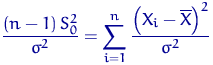 имеет
имеет
Взгляните: вопреки определению 16 распределения ![]() ,
величина
,
величина ![]() — сумма не
— сумма не ![]() , а
, а ![]() слагаемых,
причем эти слагаемые зависимы из-за присутствия в каждом
слагаемых,
причем эти слагаемые зависимы из-за присутствия в каждом ![]() .
К тому же
они хоть и одинаково распределены, но их распределение — не
.
К тому же
они хоть и одинаково распределены, но их распределение — не ![]() .
а какое? разыскать!
Надеемся, что внимательный читатель, помня, что в невырожденном случае
величины
.
а какое? разыскать!
Надеемся, что внимательный читатель, помня, что в невырожденном случае
величины ![]() и
и ![]() всегда зависимы, и видя,
как в выражении для
всегда зависимы, и видя,
как в выражении для ![]() явным образом
участвует
явным образом
участвует ![]() , придет в неподдельный восторг от независимости
, придет в неподдельный восторг от независимости
![]() и
и ![]() .
.
Доказательство основного следствия леммы Фишера
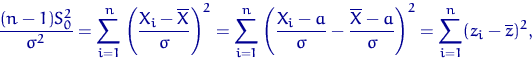
где ![]() имеют стандартное нормальное распределение,
и
имеют стандартное нормальное распределение,
и ![]() . Т.е. можно с самого начала считать, что
. Т.е. можно с самого начала считать, что ![]() имеют стандартное нормальное распределение,
и доказывать пункт 2 следствия при
имеют стандартное нормальное распределение,
и доказывать пункт 2 следствия при ![]() ,
, ![]() .
.
Применим лемму Фишера.
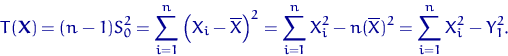
Мы обозначили через ![]() величину
величину
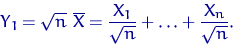
Чтобы применить лемму Фишера,
нужно найти ортогональную матрицу ![]() такую, что
такую, что
![]() — первая координата вектора
— первая координата вектора ![]() . Возьмем матрицу
. Возьмем матрицу ![]() с первой строкой
с первой строкой
![]() . Так как длина (норма) этого вектора — единица, его можно дополнить до
ортонормального базиса в
. Так как длина (норма) этого вектора — единица, его можно дополнить до
ортонормального базиса в ![]() (иначе — этот столбец можно дополнить до ортогональной матрицы).
Тогда
(иначе — этот столбец можно дополнить до ортогональной матрицы).
Тогда ![]() и будет первой координатой вектора
и будет первой координатой вектора
![]() .
.
Осталось применить лемму Фишера. непременно сделайте это!
Q.D.E.
Очередное следствие из леммы Фишера наконец позволит нам строить доверительные интервалы для параметров нормального распределения — то, ради чего мы и доказали уже так много утверждений. В каждом пункте указано, для какого параметра мы построим доверительный интервал с помощью данного утверждения.
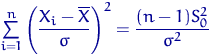 имеет распределение
имеет распределение 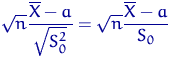 имеет распределение
имеет распределение Доказательство следствия. 1) и 3) — из леммы Фишера, 2) — из следствия 3. Осталось воспользоваться леммой Фишера и определением 17 распределения Стьюдента, чтобы доказать 4).
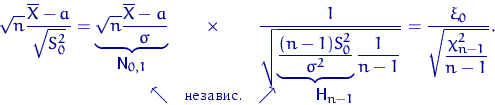
Q.D.E.