Многомерное нормальное распределение

Определение 33.

Пусть случайный вектор $\text{\boldmath\ensuremath \xi}=(\xi_1,\ldots,\xi_m)$ имеет вектор средних ${\mathbf a}={\mathsf E}\,\text{\boldmath\ensuremath \xi}$ и невырожденную матрицу ковариаций $\Sigma$ , составленную из элементов $\Sigma_{ij}=\mathop{cov}(\xi_i,\xi_j)$ . Говорят, что вектор $\text{\boldmath\ensuremath \xi}$ имеет нормальное распределение ${\mathsf N}_{{\mathbf a},\Sigma}$ в ${\textrm{\upshape I\kern-0.20em R}}^m$ , если плотность этого вектора равна

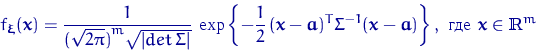
$\begin{displaymath} f_{\text{\boldmath\ensuremath \xi}}({\mathbf x})= \dfrac{1}{... ...xtrm{ где } {\mathbf x}\in{\textrm{\upshape I\kern-0.20em R}}^m\end{displaymath}$

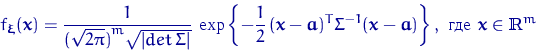
Квадратичная форма $({\mathbf x}-{\mathbf a})^T \Sigma^{-1} ({\mathbf x}-{\mathbf a})$ в показателе экспоненты равна

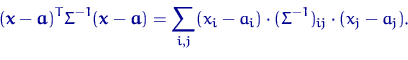$\begin{equation} ({\mathbf x}-{\mathbf a})^T \Sigma^{-1} ({\mathbf x}-{\mathbf a})= \sum_{i,j}(x_i-a_i)\cdot(\Sigma^{-1})_{ij}\cdot(x_j-a_j).\end{equation}$

(37)

Замечание 24.

Вектор, составленный из нормальных случайных величин, не обязательно имеет многомерное нормальное распределение. Так, вектор $(\xi, c\xi)$ имеет вырожденную матрицу ковариаций $\left(\begin{smallmatrix} 1 & c\cr c & ~c^2\end{smallmatrix}\right)$ , если ${\mathsf D}\,\xi=1$ , и не имеет плотности в ${\textrm{\upshape I\kern-0.20em R}}^2$ .

Поэтому в условиях следующей теоремы существование совместной нормальной плотности координат вектора обязательно.

Теорема 14.

Пусть вектор $\text{\boldmath\ensuremath \xi}$ имеет многомерное нормальное распределение ${\mathsf N}_{{\mathbf a},\Sigma}$ . Координаты этого вектора независимы тогда и только тогда, когда они некоррелированы, т.е. когда матрица ковариаций $\Sigma$ диагональна.

Замечание 25.

Следовало бы крикнуть «ура!»: свойство, о котором мы давно мечтали, — чтобы независимость следовала из некоррелированности, — имеет все же место. Но только для наборов случайных величин с нормальным совместным распределением, и это — очередное изумительное качество нормального распределения.

Только в случае диагональной матрицы $\Sigma$ с элементами $\Sigma_{ii}=\sigma_i^2={\mathsf D}\,\xi_i$ квадратичная форма (37) превращается в сумму квадратов

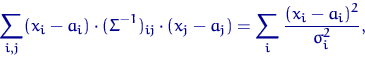
$\begin{displaymath} \sum_{i,j}(x_i-a_i)\cdot(\Sigma^{-1})_{ij}\cdot(x_j-a_j)= \sum_i\dfrac{(x_i-a_i)^2}{\sigma_i^2},\end{displaymath}$

и многомерная плотность распадается в произведение плотностей координат.

Надеюсь, читатель поверит следующей теореме без доказательства, будучи в состоянии доказать ее, как и в одномерном случае, с помощью многомерных характеристических функций.

Многомерная центральная предельная теорема.

Пусть $\text{\boldmath\ensuremath \xi}^{(1)},\text{\boldmath\ensuremath \xi}^{(2)},\ldots$ — последовательность независимых и одинаково распределенных случайных векторов, каждый из которых имеет среднее ${\mathsf E}\,\text{\boldmath\ensuremath \xi}^{(1)}{=}{\mathbf a}$ и невырожденную матрицу ковариаций $\Sigma$ . Обозначим через $S_n=\text{\boldmath\ensuremath \xi}^{(1)}{+}\ldots{+}\text{\boldmath\ensuremath \xi}^{(n)}$ вектор частичных сумм.

Тогда при $n\to\infty$ имеет место слабая сходимость распределений векторов

$\begin{displaymath} \text{\boldmath\ensuremath \eta}^{(n)}=\dfrac{S_n-n{\mathbf ... ...textrm{имеет распределение } {\mathsf N}_{{\mathbf 0},\Sigma}.\end{displaymath}$ , где имеет распределение .

В условиях многомерной ЦПТ распределение любых непрерывных функций $g\left(\text{\boldmath\ensuremath \eta}^{(n)}\right)$ слабо сходится к распределению $g(\text{\boldmath\ensuremath \eta})$ . В качестве $g({\mathbf x})$ нам будет нужна только $g({\mathbf x})=\sum x_i^2=\lVert {\mathbf x} \rVert^2$ .

Следствие 5.

В условиях многомерной ЦПТ имеет место сходимость $\lVert \text{\boldmath\ensuremath \eta}^{(n)} \rVert^2 \Rightarrow \lVert \text{\boldmath\ensuremath \eta} \rVert^2$ .

10.1. Многомерное нормальное распределение