Если ![]() ,
, ![]() ,
, ![]() независимы и имеют стандартное нормальное
распределение, то случайная величина
независимы и имеют стандартное нормальное
распределение, то случайная величина
![]()
имеет гамма-распределение ![]() .
.
Из свойства 7 и свойства 8 непосредственно следует утверждение:
Если ![]() ,
, ![]() ,
, ![]() независимы и имеют стандартное нормальное
распределение, то случайная величина
независимы и имеют стандартное нормальное
распределение, то случайная величина
![]()
имеет гамма-распределение ![]() .
.
Распределение суммы ![]() квадратов независимых
стандартных нормальных случайных величин называют
распределением «хи-квадрат» с
квадратов независимых
стандартных нормальных случайных величин называют
распределением «хи-квадрат» с ![]() степенями свободы
и обозначают
степенями свободы
и обозначают ![]() . Согласно следствию 2, распределение
. Согласно следствию 2, распределение ![]() совпадает с
совпадает с ![]() .
.
На графике ниже изображены плотности распределения ![]() при
при ![]() равном 1, 2, 4 и 8.
равном 1, 2, 4 и 8.
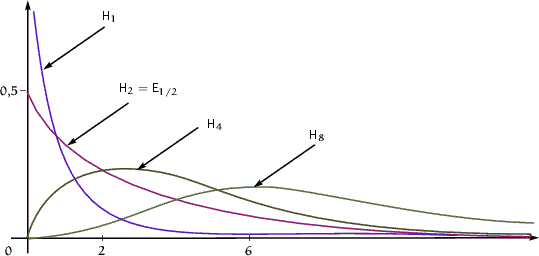 | Вид плотности |
Мы часто будем обозначать через ![]() случайную
величину с распределением
случайную
величину с распределением ![]() .
.
Рассмотрим свойства ![]() -распределения:
-распределения:
Пусть случайная величина
![]() имеет распределение
имеет распределение ![]() , случайная величина
, случайная величина ![]() имеет
распределение
имеет
распределение ![]() , причем эти случайные величины независимы.
Тогда их сумма
, причем эти случайные величины независимы.
Тогда их сумма ![]() имеет распределение
имеет распределение
![]() .
.
![]()
а их сумма — как
![]() , т.е. имеет распределение
, т.е. имеет распределение ![]() .
.
Q.D.E.
Если ![]() имеет распределение
имеет распределение ![]() ,
то
,
то
![]()
![]()
(см. пример 20). Поэтому
![]()
Q.D.E.
Если ![]() ,
, ![]() ,
, ![]() независимы и имеют
нормальное распределение
независимы и имеют
нормальное распределение ![]() , то
, то
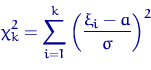
имеет ![]() -распределение
-распределение ![]() с
с ![]() степенями свободы.
степенями свободы.
N.I.Chernova