Пусть ![]() имеет распределение
имеет распределение ![]() , а
— распределение
, а
— распределение ![]() , причем
эти случайные величины независимы.
Распределение случайной величины
, причем
эти случайные величины независимы.
Распределение случайной величины
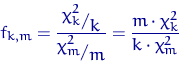
называют
распределением Фишера с ![]() ,
, ![]() степенями свободы
и обозначают
степенями свободы
и обозначают ![]() .
.
Пусть ![]() имеет распределение
имеет распределение ![]() , а
— распределение
, а
— распределение ![]() , причем
эти случайные величины независимы.
Распределение случайной величины
, причем
эти случайные величины независимы.
Распределение случайной величины
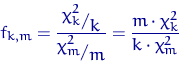
называют
распределением Фишера с ![]() ,
, ![]() степенями свободы
и обозначают
степенями свободы
и обозначают ![]() .
.
Свойства распределения Фишера (или Фишера — Снедекора):
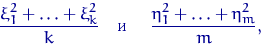
сходится к 1 по вероятности при ![]() ,
, ![]() .
Здесь
.
Здесь ![]() ,
, ![]() ,
, ![]() и
и
![]() ,
, ![]() ,
, ![]() — независимые последовательности, составленные из
независимых случайных величин со стандартным нормальным распределением.
— независимые последовательности, составленные из
независимых случайных величин со стандартным нормальным распределением.
Q.D.E.
N.I.Chernova