![]()
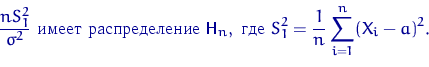
Пусть ![]() и
и ![]() — квантили распределения
— квантили распределения ![]() уровня
уровня ![]() и
и ![]() . Тогда
. Тогда
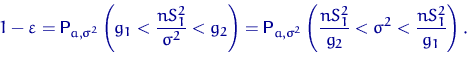
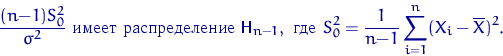
Пусть ![]() и
и ![]() — квантили распределения
— квантили распределения ![]() уровня
уровня ![]() и
и ![]() . Тогда
. Тогда
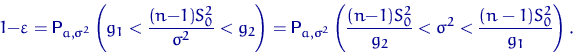
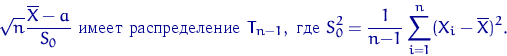
Пусть ![]() и
и ![]() — квантили распределения
— квантили распределения ![]() уровня
уровня ![]() и
и ![]() . Распределение Стьюдента симметрично, поэтому
. Распределение Стьюдента симметрично, поэтому
![]() . Тогда
. Тогда
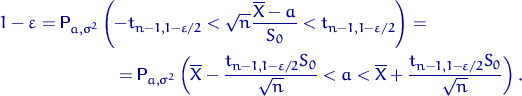
![]()
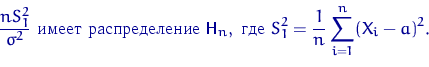
Пусть ![]() и
и ![]() — квантили распределения
— квантили распределения ![]() уровня
уровня ![]() и
и ![]() . Тогда
. Тогда
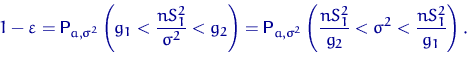
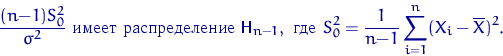
Пусть ![]() и
и ![]() — квантили распределения
— квантили распределения ![]() уровня
уровня ![]() и
и ![]() . Тогда
. Тогда
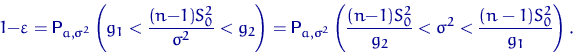
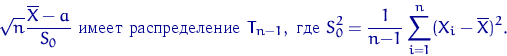
Пусть ![]() и
и ![]() — квантили распределения
— квантили распределения ![]() уровня
уровня ![]() и
и ![]() . Распределение Стьюдента симметрично, поэтому
. Распределение Стьюдента симметрично, поэтому
![]() . Тогда
. Тогда
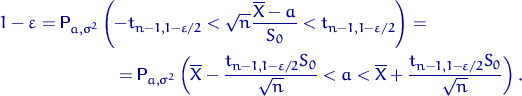
Доверительные интервалы, полученные в п. 2
и 3, выглядят странно по сравнению с ДИ из п. 1 и 4: они
содержат ![]() в числителе, а не в знаменателе. Но если квантили нормального
распределения от
в числителе, а не в знаменателе. Но если квантили нормального
распределения от ![]() не зависят вовсе, квантили распределения Стьюдента
асимптотически не зависят от
не зависят вовсе, квантили распределения Стьюдента
асимптотически не зависят от ![]() по свойству
по свойству ![]() , то квантили распределения
, то квантили распределения ![]() зависят от
зависят от ![]() существенно. Действительно,
пусть
существенно. Действительно,
пусть ![]() таково, что
таково, что
![]() при всех
при всех ![]() , в том числе и при
, в том числе и при ![]() .
Тогда последовательность
.
Тогда последовательность ![]() такова, что
такова, что
![]() при
при ![]() , где
, где ![]() — квантиль стандартного нормального распределения.
В самом деле: по ЦПТ с ростом
— квантиль стандартного нормального распределения.
В самом деле: по ЦПТ с ростом ![]()
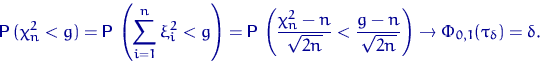
Поэтому квантиль уровня ![]() распределения
распределения ![]() ведет себя как
ведет себя как
![]() .
.
N.I.Chernova