- 1.
- Построить какую-нибудь вероятность
на множестве натуральных чисел как на дискретном пространстве элементарных исходов.
- 2.
- Вероятность события
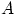 равна нулю. Верно ли, что тогда
равна нулю. Верно ли, что тогда 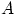 — невозможное событие?
— невозможное событие?
- 3.
- Являются ли события «выпал герб при первом броске монеты» и
«выпал герб при втором броске монеты» несовместными?
- 4.
- Пусть
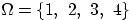 . Является ли алгеброй набор множеств
. Является ли алгеброй набор множеств
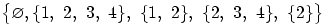 ?
?
- 5.
- Задать какую-нибудь алгебру на множестве
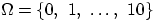 .
.
- 6.
- Пусть
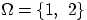 . На множестве
. На множестве 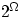 задана функция:
задана функция:
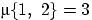 ,
, 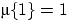 ,
, 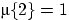 . Является ли
. Является ли 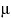 мерой?
мерой?
- 7.
- Задать какую-нибудь вероятностную меру на множестве всех подмножеств
множества
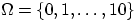 (как на сигма-алгебре).
(как на сигма-алгебре).
- 8.
- Является ли
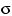 -алгеброй декартово произведение
-алгеброй декартово произведение
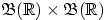 двух борелевских
двух борелевских
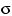 -алгебр?
-алгебр?
- 9.
- Принадлежит ли множество
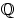 рациональных чисел
рациональных чисел 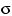 -алгебре,
порождённой множеством всех одноточечных подмножеств
-алгебре,
порождённой множеством всех одноточечных подмножеств 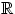 ?
?
- 10.
- На борелевской
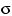 -алгебре в
-алгебре в 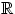 задана функция:
задана функция:
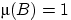 для любого
для любого 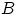 . Является ли
. Является ли 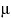 вероятностной мерой?
вероятностной мерой?
- 11.
- Пусть функция
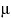 на множестве
на множестве 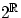 задана так:
задана так:
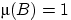 , если
, если 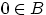 , и
, и 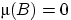 , если
, если 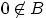 .
Является ли функция
.
Является ли функция 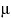 мерой на множестве всех подмножеств
мерой на множестве всех подмножеств 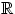 ?
?
- 12.
- Привести пример какой-нибудь меры,
отличной от меры Лебега, на
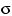 -алгебре
-алгебре 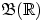 борелевских множеств на прямой.
борелевских множеств на прямой.
См. определения 28, 29, 30 и т.д.
- 13.
- Доказать, что если
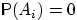 для всех
для всех 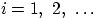 ,
то
,
то
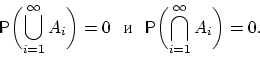
См. свойства вероятности 4 и
7.
- 14.
- Доказать, что если
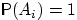 для всех
для всех 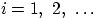 ,
то
,
то
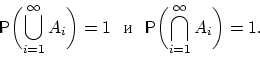
См. свойства вероятности 4 и
7.
- 15.
- Найти количество всех 2005-значных чисел, в записи которых используются все цифры от
1 до 9, но никакие соседние цифры в записи этих чисел не совпадают.
См. формулу включения-исключения.
- 16.
- Найти вероятность того, что при раздаче колоды в 52 карты четверым
игрокам поровну хотя бы у одного из игроков соберутся все карты одной масти.
См. формулу включения-исключения.
- 17.
- Доказать, что
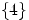 является борелевским множеством.
является борелевским множеством.
- 18.
- Доказать, что
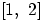 является борелевским множеством.
является борелевским множеством.
- 19.
- Доказать, что канторовское совершенное множество является борелевским множеством.
См. определения 13 и 11.
- 20.
- Могут ли два независимых события образовать полную группу событий?
- 21.
- Из полной колоды карт вынимают одну. Будут ли независимыми события
«вынутая карта — король» и «вынутая карта — туз»?
- 22.
- Что означает независимость в совокупности событий
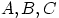 и
и 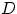 ?
?
- 23.
- Следует ли из равенства
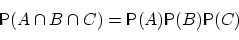
независимость событий 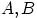 и
и 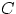 в совокупности? Если «да» — доказать, если
«нет» — привести контрпример.
в совокупности? Если «да» — доказать, если
«нет» — привести контрпример.
- 24.
- Следует ли из того же равенства попарная независимость
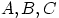 ? Если «да» — доказать, если
«нет» — привести контрпример.
? Если «да» — доказать, если
«нет» — привести контрпример.
- 25.
- Пусть
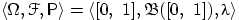 , где
, где 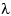 — мера Лебега. Построить на этом вероятностном пространстве три
случайных величины с равномерными на [0, 1] распределениями.
— мера Лебега. Построить на этом вероятностном пространстве три
случайных величины с равномерными на [0, 1] распределениями.
- 26.
- Пусть
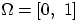 ,
, 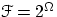 ,
, 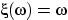 .
Задать вероятностную меру
.
Задать вероятностную меру 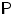 так, чтобы функция
так, чтобы функция  оказалась случайной величиной с вырожденным
распределением.
оказалась случайной величиной с вырожденным
распределением.
- 27.
- Пусть
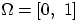 ,
, 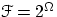 ,
, 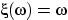 .
Задать вероятностную меру
.
Задать вероятностную меру 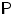 так, чтобы функция
так, чтобы функция  оказалась случайной величиной с распределением
Бернулли.
оказалась случайной величиной с распределением
Бернулли.
- 28.
- Привести пример вероятностного пространства и на нем трёх
независимых попарно, но зависимых в совокупности случайных величин.
- 29.
- Доказать, что случайная величина с вырожденным распределением
независима с любой другой случайной величиной.
- 30.
- Пусть случайная величина
 имеет стандартное
нормальное распределение, а случайная величина
имеет стандартное
нормальное распределение, а случайная величина  равна знаку
равна знаку  .
Проверить, независимы ли случайные величины
.
Проверить, независимы ли случайные величины 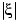 и
и  .
.
- 31.
- Доказать, что из независимости в совокупности
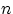 случайных
величин следует их попарная независимость.
случайных
величин следует их попарная независимость.
- 32.
- Доказать, что случайные величины
 и
и  независимы тогда и только тогда,
когда для любых двух борелевских функций
независимы тогда и только тогда,
когда для любых двух борелевских функций 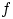 и
и 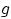 независимы случайные величины
независимы случайные величины
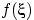 и
и 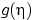 .
.
- 33.
- Может ли какое-нибудь из стандартных дискретных
распределений быть устойчивым относительно:
а) умножения на некоторую постоянную?
б) умножения на произвольную постоянную?
в) произвольного линейного преобразования?
Здесь устойчивость — сохранение того же вида распределения.
- 34.
- Какие из стандартных абсолютно-непрерывных распределений
устойчивы относительно:
а) умножения на некоторую постоянную?
б) умножения на произвольную постоянную?
в) произвольного линейного преобразования?
- 35.
- Привести пример случайных величин
 и
и  с одинаковым нормальным
распределением, сумма которых имеет вырожденное распределение.
с одинаковым нормальным
распределением, сумма которых имеет вырожденное распределение.
- 36.
- Привести пример случайных величин
 и
и  с пуассоновскими
распределениями, сумма которых имеет распределение, отличное от пуассоновского.
с пуассоновскими
распределениями, сумма которых имеет распределение, отличное от пуассоновского.
- 37.
- Привести пример случайных величин
 и
и  с пуассоновскими
распределениями с параметрами
с пуассоновскими
распределениями с параметрами 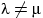 , сумма которых имеет
распределение, отличное от пуассоновского.
, сумма которых имеет
распределение, отличное от пуассоновского.
См. пример 49.
- 38.
- Пусть
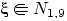 и
и 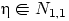 — независимые случайные величины.
Какое распределение имеет
— независимые случайные величины.
Какое распределение имеет 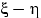 ?
?
- 39.
- Когда возможно равенство
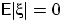 ?
?
- 40.
- Пусть четвёртый момент случайной величины
 конечен,
и имеет место равенство
конечен,
и имеет место равенство 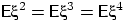 .
Доказать, что
.
Доказать, что
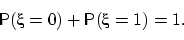
Распределение Бернулли, и только оно, обладает свойством 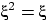 .
.
- 41.
- Привести пример случайной величины с дискретным
распределением, у которой существует первый момент, но не существует
дисперсия.
- 42.
- Сравнить
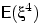 и
и 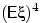 .
.
- 43.
- Привести пример случайной величины с абсолютно непрерывным
распределением, у которой существует второй момент, но не существует
третий.
- 44.
- Привести пример случайных величин
 и
и  таких,
что
таких,
что 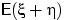 существует, но ни
существует, но ни 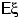 , ни
, ни
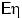 не существуют.
не существуют.
- 45.
- Привести пример случайных величин
 и
и  таких,
что
таких,
что 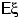 и
и 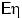 существуют, но не существует
существуют, но не существует
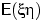 .
. - 46.
- Привести пример одинаково распределённых случайных величин
 ,
,  и
и 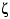 таких,
что все три величины
таких,
что все три величины 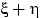 ,
, 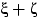 и
и 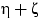 имеют различные
распределения.
имеют различные
распределения.
Достаточно, если каждая будет принимать три значения.
- 47.
- Привести пример одинаково распределённых случайных величин
 и
и  таких,
что величины
таких,
что величины 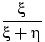 и
и 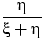 имеют разные
распределения.
имеют разные
распределения.
- 48.
- Привести пример, показывающий что для одинаково распределённых
случайных величин
 и
и  не обязательно
не обязательно
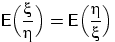 , даже если эти математические ожидания существуют.
, даже если эти математические ожидания существуют.
- 49.
- Привести пример, показывающий,
что следующее утверждение неверно: «Для любых унимодальных
распределений медиана всегда лежит между математическим ожиданием и модой».
Попробуйте распределение с плотностью
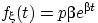 при
при 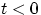 и
и
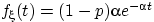 при
при 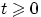 , где
, где 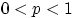 ,
,
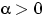 ,
, 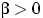 — параметры.
— параметры.
- 50.
- Привести пример того, что в ЗБЧ Хинчина существенно
условие независимости.
- 51.
- Проверить, имеет ли место сходимость
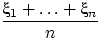 к нулю по вероятности
для последовательности
к нулю по вероятности
для последовательности 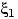 ,
, 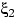 ,... независимых случайных величин
со стандартным распределением Коши.
,... независимых случайных величин
со стандартным распределением Коши.
- 52.
- Пусть
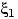 ,
, 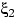 , ... — последовательность
независимых и одинаково распределённых случайных величин с невырожденным распределением.
Доказать, что не существует случайной величины
, ... — последовательность
независимых и одинаково распределённых случайных величин с невырожденным распределением.
Доказать, что не существует случайной величины  , к которой данная
последовательность сходилась бы по вероятности. Сходится ли эта
последовательность по распределению?
, к которой данная
последовательность сходилась бы по вероятности. Сходится ли эта
последовательность по распределению?
- 53.
- Доказать, что в условиях ЦПТ последовательность
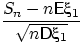 не сходится по вероятности
ни к какой случайной величине.
не сходится по вероятности
ни к какой случайной величине.
Рассмотрите отдельно и вместе сумму первых и следующих 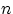 слагаемых.
слагаемых.
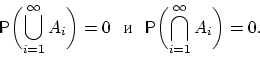
![]()
![]() и
и ![]() в совокупности? Если «да» — доказать, если
«нет» — привести контрпример.
в совокупности? Если «да» — доказать, если
«нет» — привести контрпример.
![]()
![]() .
.
![]() при
при ![]() и
и
![]() при
при ![]() , где
, где ![]() ,
,
![]() ,
, ![]() — параметры.
— параметры.
![]() слагаемых.
слагаемых.