Доказательство теоремы Пирсона

Next: Алфавитный указатель Up: Добавления Previous: Многомерное нормальное распределение

10.2. Доказательство теоремы Пирсона

План действий:

1. Сначала покажем, что величина $\rho=\sum_{j=1}^k {(\nu_j-np_j)^2}/{np_j}$ есть квадрат нормы некоторого вектора $\text{\boldmath\ensuremath \eta}^{(n)}=(S_n-n{\mathbf a})/\!\sqrt{n}$ в ${\textrm{\upshape I\kern-0.20em R}}^k$ . Затем убедимся в том, что матрица ковариаций типичного слагаемого $\text{\boldmath\ensuremath \xi}^{(1)}$ в сумме вырождена, что мешает использовать многомерную ЦПТ.

2. Найдем ортогональное преобразование , приводящее $\text{\boldmath\ensuremath \xi}^{(1)}$ к виду

$C\cdot\text{\boldmath\ensuremath \xi}^{(1)}=(\hat{\text{\boldmath\ensuremath \xi}}^{(1)},0)$ ,

где вектор уже имеет невырожденную единичную матрицу ковариаций. В силу линейности умножения, вектор $\text{\boldmath\ensuremath \eta}^{(n)}$ тоже перейдет в вектор $C\cdot\text{\boldmath\ensuremath \eta}^{(n)}=(\hat{\text{\boldmath\ensuremath \eta}}^{(n)},0)$ с нулевой последней координатой. Но его норма не изменится из-за ортогональности матрицы .

3. К вектору сумм $\hat{\text{\boldmath\ensuremath \eta}}^{(n)}$ применим многомерную ЦПТ. В пределе получим -мерный нормальный вектор с нулевым средним и единичной матрицей ковариаций, т.е. составленный из независимых величин со стандартным нормальным распределением. Воспользуемся следствием 5 и тем, что квадрат нормы этого вектора имеет $\chi^2$ -распределение ${\mathsf H}_{k-1}$ .

Реализация:

1. С каждым элементом выборки свяжем вектор-столбец $\text{\boldmath\ensuremath \xi}^{(i)}$ :

$\begin{displaymath} \text{\boldmath\ensuremath \xi}^{(i)}=(\xi_1,\ldots,\xi_k)=\... ...f I}(X_i\in A_k)-p_k}{\sqrt{p_k}}\right), \quad i=1,2,\ldots,n.\end{displaymath}$

Получим независимых и одинаково распределенных векторов. Среднее ${\mathbf a}={\mathsf E}\,\text{\boldmath\ensuremath \xi}^{(1)}$ равно нулю, поскольку ${\mathsf E}\,{\mathbf I}(X_1\in A_j)=p_j$ для любого $j=1,\ldots,k$ .

Далее, $\nu_j = \sum_{i=1}^n {\mathbf I}(X_i\in A_j)$ , поэтому

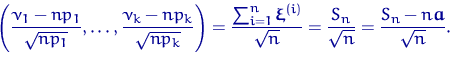
$\begin{displaymath} \left(\dfrac{\nu_1-np_1}{\sqrt{np_1}},\ldots, \dfrac{\nu_k-n... ...{n}}=\dfrac{S_n}{\sqrt{n}}= \dfrac{S_n-n{\mathbf a}}{\sqrt{n}}.\end{displaymath}$

Найдем матрицу ковариаций вектора $\text{\boldmath\ensuremath \xi}^{(1)}$ , составленную из элементов

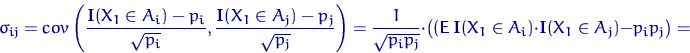
$\begin{displaymath} \sigma_{ij}=\mathop{cov} \left(\dfrac{{\mathbf I}(X_1\in A_i... ...mathbf I}(X_1\in A_i)\cdot{\mathbf I}(X_1\in A_j)-p_ip_j\bigr)=\end{displaymath}$

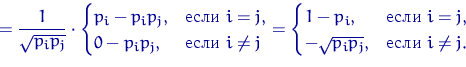
$\begin{displaymath} =\dfrac{1}{\sqrt{p_ip_j}}\cdot \begin{cases} p_i-p_ip_j, & \... ... } i=j, \cr -\sqrt{p_ip_j}, & \textrm{если } i\ne j.\end{cases}\end{displaymath}$

Вырождена эта матрица хотя бы оттого, что координаты вектора $\text{\boldmath\ensuremath \xi}^{(1)}$ линейно связаны:

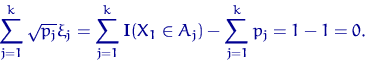$\begin{equation} \sum_{j=1}^k \sqrt{p_j}\xi_j=\sum_{j=1}^k {\mathbf I}(X_1\in A_j)-\sum_{j=1}^k p_j=1-1=0.\end{equation}$ (38)

2. Из (38) мораль: если последняя строка ортогональной матрицы будет иметь вид $(\sqrt{p_1},\ldots,\sqrt{p_k}\,)$ (что вполне возможно — норма такой строки равна единице), то после умножения на $\text{\boldmath\ensuremath \xi}^{(1)}$ получим вектор с нулевой последней координатой — в точности (38).

При умножении вектора $\text{\boldmath\ensuremath \xi}$ на матрицу слева его матрица ковариаций $\Sigma={\mathsf E}\,\text{\boldmath\ensuremath \xi}\text{\boldmath\ensuremath \xi}^T$ перейдет в $B=C\Sigma C^T$ . Убедимся, что, какой бы ни была ортогональная матрица , в результате получим диагональную матрицу из нулей с единицами на главной диагонали, кроме элемента $b_{kk}=0$ . Ортогональность означает, что для любых $m\ne k$ и $l\ne m$ имеют место равенства

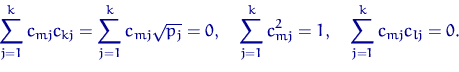
$\begin{displaymath} \sum_{j=1}^k c_{mj}c_{kj}=\sum_{j=1}^k c_{mj}\sqrt{p_j}=0, \quad \sum_{j=1}^k c_{mj}^2=1, \quad \sum_{j=1}^k c_{mj}c_{lj}=0.\end{displaymath}$

Учитывая, что -й элемент матрицы есть $c_{li}$ , получим

$\begin{displaymath} b_{ml}=\sum_{i=1}^k\left(\sum_{j=1}^k c_{mj}\sigma_{ji}\righ... ...sum_{j\ne i} -c_{mj}\sqrt{p_ip_j}+c_{mi}(1-p_i)\right) c_{li}=\end{displaymath}$

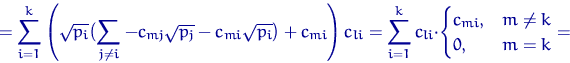
$\begin{displaymath} =\sum_{i=1}^k\left(\sqrt{p_i}\bigl( \sum_{j\ne i} -c_{mj}\sq... ...\cdot \begin{cases} c_{mi}, & m\ne k \cr 0, & m=k\end{cases} =\end{displaymath}$

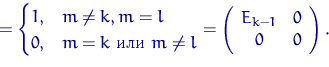$\begin{equation} = \begin{cases} 1, & m\ne k, m=l \cr 0, & m=k \textrm{ или } m... ... \left( \begin{array} {cc}E_{k-1} & 0 \cr 0 & 0\end{array}\right).\end{equation}$ (39)

3. Осталось повторить то, что мы уже описали в плане: умножение $C\cdot\text{\boldmath\ensuremath \xi}^{(1)}=(\hat{\text{\boldmath\ensuremath \xi}}^{(1)},0)$ приводит к вектору с нулевой последней координатой по (38). Равенствами (39) мы показали, что вектор имеет невырожденную единичную матрицу ковариаций $E_{k-1}$ . Вектора независимы, одинаково распределены, имеют нулевое среднее $C\cdot{\mathsf E}\,\text{\boldmath\ensuremath \xi}^{(1)}={\mathbf 0}$ .

Все условия многомерной ЦПТ выполнены, поэтому

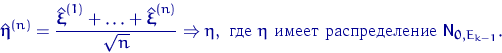
$\begin{displaymath} \hat{\text{\boldmath\ensuremath \eta}}^{(n)}=\dfrac{\hat{\te... ...\space имеет распределение } {\mathsf N}_{{\mathbf 0},E_{k-1}}.\end{displaymath}$

По следствию 5, норма вектора $\hat{\text{\boldmath\ensuremath \eta}}^{(n)}$ слабо сходится к норме вектора $\eta$ , состоящего, согласно теореме 14, из независимых случайных величин со стандартным нормальным распределением:

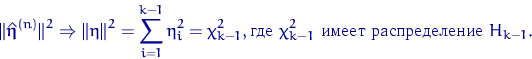$\begin{equation} \lVert \hat{\text{\boldmath\ensuremath \eta}}^{(n)}\rVert^2\Rig... ..., \textrm{где $\chi^2_{k-1}$\space имеет распределение } H_{k-1}.\end{equation}$ (40)

Распределение ${\mathsf H}_{k-1}$ возникло здесь по определению 16. Осталось заметить, что у векторов $\text{\boldmath\ensuremath \eta}^{(n)}$ , $C\cdot\text{\boldmath\ensuremath \eta}^{(n)}$ , $\hat{\text{\boldmath\ensuremath \eta}}^{(n)}$ , связанных равенствами

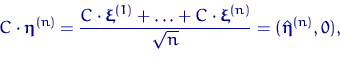
$\begin{displaymath} C\cdot\text{\boldmath\ensuremath \eta}^{(n)}=\dfrac{C\cdot\t... ...}{\sqrt{n}} =(\hat{\text{\boldmath\ensuremath \eta}}^{(n)},0), \end{displaymath}$

нормы одинаковы в силу (17): $\lVert \text{\boldmath\ensuremath \eta}^{(n)}\rVert^2=\lVert C\cdot \text{\bold... ...}}^{(n)},0)\rVert^2=\lVert \hat{\text{\boldmath\ensuremath \eta}}^{(n)}\rVert^2$ . И все эти нормы ведут себя так же как и (40).

Упражнение. Найти среди этих норм величину $\rho$ из теоремы Пирсона.

Q.D.E.

N.I.Chernova 9 сентября 2002