Введем два вектора: ![]() — факторы регрессии и
— факторы регрессии и
![]() -- неизвестные параметры регрессии.
Каждый вектор есть вектор-столбец,
а изображен по горизонтали для удобства.
Обозначать вектора мы, как и ранее, будем жирным шрифтом.
-- неизвестные параметры регрессии.
Каждый вектор есть вектор-столбец,
а изображен по горизонтали для удобства.
Обозначать вектора мы, как и ранее, будем жирным шрифтом.
Рассматривается модель регрессии, которая в курсе «Эконометрика» называется простой (линейной) регрессией:
![]()
Пусть в ![]() -м эксперименте факторы регрессии принимают заранее заданные
значения
-м эксперименте факторы регрессии принимают заранее заданные
значения ![]() , где
, где ![]() .
.
После ![]() экспериментов получен набор
откликов
экспериментов получен набор
откликов ![]() , где
, где
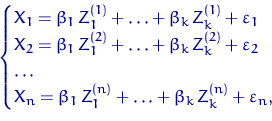
или, в матричной форме, ![]() , где матрица
, где матрица ![]() (матрица плана) равна
(матрица плана) равна
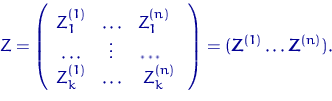
Вектор ![]() состоит
из случайных ошибок в данных экспериментах.
состоит
из случайных ошибок в данных экспериментах.
Требуется по данным матрице плана ![]() и вектору результатов
и вектору результатов ![]() найти оценки для параметров регрессии
найти оценки для параметров регрессии ![]() и параметров
распределения вектора
ошибок
и параметров
распределения вектора
ошибок ![]() .
.
N.I.Chernova