Пусть ![]() — выборка объема
— выборка объема ![]() из неизвестного
распределения
из неизвестного
распределения ![]() с функцией распределения
с функцией распределения ![]() . Пусть
. Пусть ![]() — эмпирическая функция распределения, построенная по
этой выборке.
Тогда для любого
— эмпирическая функция распределения, построенная по
этой выборке.
Тогда для любого ![]()
![]()
Мы ввели три вида эмпирических характеристик, предназначенных для оценивания неизвестных теоретических характеристик распределения: эмпирическую функцию распределения, гистограмму, выборочные моменты. Если наши оценки удачны, разница между ними и истинными характеристиками должна стремится к нулю с ростом объема выборки. Такое свойство эмпирических характеристик называют состоятельностью. Убедимся, что наши выборочные характеристики таким свойством обладают.
Пусть ![]() — выборка объема
— выборка объема ![]() из неизвестного
распределения
из неизвестного
распределения ![]() с функцией распределения
с функцией распределения ![]() . Пусть
. Пусть ![]() — эмпирическая функция распределения, построенная по
этой выборке.
Тогда для любого
— эмпирическая функция распределения, построенная по
этой выборке.
Тогда для любого ![]()
![]()
![]() — случайная величина, так как она является
функцией от случайных величин
— случайная величина, так как она является
функцией от случайных величин ![]() . То же самое можно
сказать про гистограмму и выборочные моменты.
. То же самое можно
сказать про гистограмму и выборочные моменты.
Доказательство теоремы 1. По определению 1,
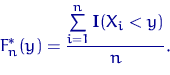
Случайные величины ![]() ,
, ![]() ,
, ![]() независимы и
одинаково распределены, их математическое ожидание конечно:
независимы и
одинаково распределены, их математическое ожидание конечно:
![]()
поэтому применим ЗБЧ Хинчина, а что это такое? и
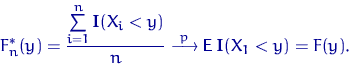
Таким образом, с ростом объема выборки эмпирическая функция распределения сходится (по вероятности) к неизвестной теоретической.
Q.D.E.
Верен более общий результат, показывающий, что сходимость эмпирической функции распределения к теоретической имеет «равномерный» характер.
Пусть ![]() — выборка объема
— выборка объема ![]() из неизвестного
распределения
из неизвестного
распределения ![]() с функцией распределения
с функцией распределения ![]() . Пусть
. Пусть ![]() — эмпирическая функция распределения, построенная по
этой выборке.
Тогда
— эмпирическая функция распределения, построенная по
этой выборке.
Тогда
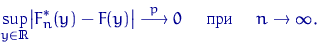
Более того, в условиях теорем 1 и Гливенко — Кантелли имеет место сходимость не только по вероятности, но и почти наверное.
Если функция распределения ![]() непрерывна, то
скорость сходимости к нулю в теореме Гливенко — Кантелли
имеет порядок
непрерывна, то
скорость сходимости к нулю в теореме Гливенко — Кантелли
имеет порядок ![]() :
:
Пусть ![]() — выборка объема
— выборка объема ![]() из неизвестного
распределения
из неизвестного
распределения ![]() с непрерывной функцией распределения
с непрерывной функцией распределения ![]() , а
, а ![]() -- эмпирическая функция распределения.
Тогда
-- эмпирическая функция распределения.
Тогда
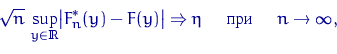
где случайная величина ![]() имеет распределение Колмогорова
с непрерывной функцией распределения
имеет распределение Колмогорова
с непрерывной функцией распределения
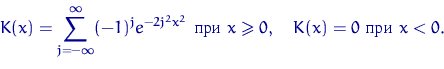
Следующие свойства эмпирической функции распределения —
это хорошо знакомые нам свойства среднего
арифметического ![]() независимых слагаемых, имеющих, к тому же, распределение
Бернулли.
независимых слагаемых, имеющих, к тому же, распределение
Бернулли.
В первых двух пунктах утверждается, что случайная величина
![]() имеет математическое ожидание
имеет математическое ожидание ![]() и
дисперсию
и
дисперсию ![]() , которая убывает как
, которая убывает как ![]() . Третий пункт показывает, что
. Третий пункт показывает, что ![]() сходится к
сходится к ![]() со скоростью
со скоростью ![]() .
.
Для любого ![]()
Доказательство свойства 1.
Заметим снова, что ![]() имеет распределение Бернулли
имеет распределение Бернулли
![]() , поэтому
, поэтому
![]()
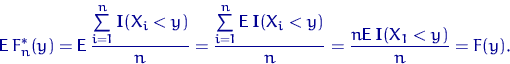
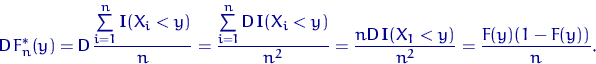
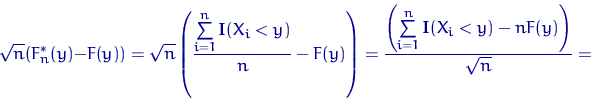
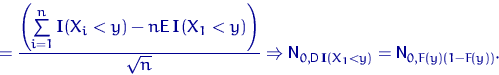
Q.D.E.
Пусть распределение ![]() абсолютно непрерывно,
абсолютно непрерывно, ![]() — его истинная
плотность.
Пусть, кроме того, число
— его истинная
плотность.
Пусть, кроме того, число ![]() интервалов группировки не зависит от
интервалов группировки не зависит от ![]() .
Случай, когда
.
Случай, когда ![]() , отмечен в замечании 1.
Справедлива
, отмечен в замечании 1.
Справедлива
Теорема утверждает, что площадь столбца гистограммы, построенного над интервалом группировки, с ростом объема выборки сближается с площадью области под графиком плотности над этим же интервалом.
Выборочное среднее ![]() является несмещенной,
состоятельной и асимптотически нормальной оценкой
для теоретического среднего (математического ожидания):
является несмещенной,
состоятельной и асимптотически нормальной оценкой
для теоретического среднего (математического ожидания):
Доказательство свойства 2
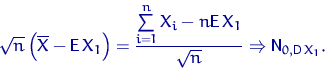
Q.D.E.
Выборочный ![]() -й момент
-й момент ![]() является несмещенной,
состоятельной и асимптотически нормальной оценкой
для теоретического
является несмещенной,
состоятельной и асимптотически нормальной оценкой
для теоретического ![]() -го момента:
-го момента:
В дальнейшем мы не будем оговаривать существование соответствующих
моментов. В частности, в первых двух пунктах следующего утверждения
предполагается наличие второго момента у случайных величин ![]() , а в третьем пункте
— четвертого (дисперсии величины
, а в третьем пункте
— четвертого (дисперсии величины ![]() ).
).
![]() .
.
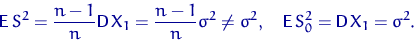
![]() .
.
Доказательство свойства 4.
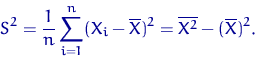 | (2) |
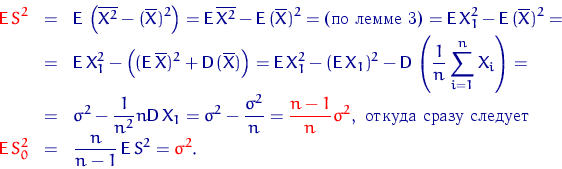
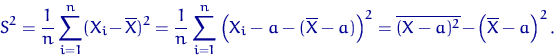
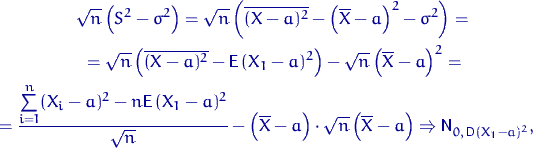
поскольку первое слагаемое слабо сходится к ![]() по ЦПТ, а второе слагаемое
по ЦПТ, а второе слагаемое
![]() слабо сходится к нулю как произведение сходящейся к нулю по вероятности последовательности и последовательности, слабо
сходящейся к
слабо сходится к нулю как произведение сходящейся к нулю по вероятности последовательности и последовательности, слабо
сходящейся к ![]() . какое свойство слабой сходимости использовано дважды?
. какое свойство слабой сходимости использовано дважды?
Q.D.E.
Next: Группированные данные Up: Основные понятия МС Previous: Выборочные моменты
N.I.Chernova