![]()
Как прежде, пусть ![]() — число элементов выборки,
попавших в интервал
— число элементов выборки,
попавших в интервал ![]() , и
, и ![]() — частота попадания
в интервал
— частота попадания
в интервал ![]() (оценка вероятности попадания в интервал):
(оценка вероятности попадания в интервал):
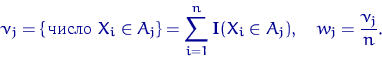
На каждом из интервалов ![]() строят прямоугольник с высотой
строят прямоугольник с высотой
![]() и получают гистограмму.
и получают гистограмму.
Рассмотрим середины интервалов: ![]() —
середина
—
середина ![]() . Набор
. Набор

можно считать «огрубленной» выборкой, в которой все ![]() , попадающие
в интервал
, попадающие
в интервал ![]() , заменены на
, заменены на ![]() . По этой выборке можно
построить такие же (но более грубые) выборочные характеристики,
что и по исходной (обозначим их так же), например выборочное
среднее
. По этой выборке можно
построить такие же (но более грубые) выборочные характеристики,
что и по исходной (обозначим их так же), например выборочное
среднее
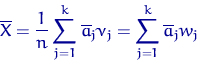
или выборочную дисперсию
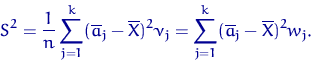
Кривая, соединяющая точки ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , называется полигоном (частот).
В отличие от гистограммы полигон — непрерывная функция (ломаная).
, называется полигоном (частот).
В отличие от гистограммы полигон — непрерывная функция (ломаная).
N.I.Chernova