Знание моментов распределения также многое может сказать о его виде и свойствах. Введем выборочные аналоги неизвестных истинных моментов распределения.
Пусть ![]() ,
, ![]() ,
, ![]() — теоретические среднее, дисперсия,
— теоретические среднее, дисперсия,
![]() -й момент. Мы уже знакомы с соответствующими характеристиками
выборочного распределения
-й момент. Мы уже знакомы с соответствующими характеристиками
выборочного распределения ![]() ,
, ![]() ,
, ![]() .
.
| Теоретические характеристики | Эмпирические характеристики |
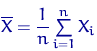 — выборочное среднее — выборочное среднее | |
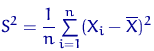 — выборочная дисперсия — выборочная дисперсия либо | |
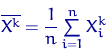 —
выборочный —
выборочный |
Список числовых характеристик и их оценок можно продолжать, рассмотрев, например, центральные, абсолютные и т.п. моменты. В общем случае
момент ![]() будем оценивать величиной
будем оценивать величиной
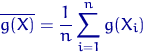 .
.
N.I.Chernova