Критерии, основанные на доверительных интервалах

Next: Исследование статистической зависимости Up: Критерии согласия Previous: Гипотеза о среднем нормальной

8.10. Критерии, основанные на доверительных интервалах

Имеется выборка ${\mathbf X}=(X_1, \ldots, X_n)$ из семейства распределений $\mathscr F_\theta$ . Проверяется простая гипотеза $H_1=\{\theta=\theta_0\}$ против сложной альтернативы $H_2=\{\theta\neq\theta_0\}$ .

Пусть имеется точный (асимптотически точный) доверительный интервал $(\theta^-,\theta^+)$ для параметра $\theta$ уровня доверия $1-\varepsilon$ . Взяв произвольное $\theta'$ , для выборки из распределения $\mathscr F_{\theta'}$ имеем

$\begin{displaymath} {\mathsf P}\,{\!}_{\theta'}(\theta^-< \theta' < \theta^+)= 1-\varepsilon \quad (\textcolor{blue}{\to 1-\varepsilon}).\end{displaymath}$

Тогда критерий

$\begin{displaymath} \delta({\mathbf X})=\begin{cases} H_1, & \textrm{если }\the... ... \textrm{если }\theta_0\not\in(\theta^-, \theta^+) \end{cases}\end{displaymath}$

имеет точный (асимптотический) размер $\varepsilon$ . Действительно,

$\begin{displaymath} \alpha_1(\delta)={\mathsf P}\,{\!}_{H_1}(\delta{=}H_2)= {\ma... ...\,\theta^+)=\varepsilon ({\textcolor{blue}{\to \varepsilon}}).\end{displaymath}$

Если доверительный интервал строится с помощью «функции отклонения» $G({\mathbf X},\theta)$ , то эта же функция годится и в качестве «функции отклонения» $\rho({\mathbf X})$ для построения критерия согласия.

Пример 33.

Посмотрим на критерий (28). Основная гипотеза принимается, только если $\lvert\rho({\mathbf X})\rvert<C=\tau_{1-\varepsilon/2}$ , что равносильно неравенству

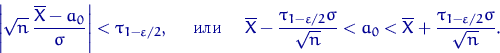
$\begin{displaymath} \left\lvert\sqrt{n}\, \dfrac{\overline X-a_0}{\sigma}\right\... ...< \overline X + \dfrac{\tau_{1-\varepsilon/2}\sigma}{\sqrt{n}}.\end{displaymath}$

Сравните то, что получилось, с точным доверительным интервалом (13) для параметра нормального распределения с известной дисперсией.

N.I.Chernova 9 сентября 2002