


Next: Критерии, основанные на ДИ
Up: Критерии согласия
Previous: Гипотеза о среднем нормальной совокупности
Проверяется та же гипотеза, что и в предыдущем разделе, но в случае, когда
дисперсия 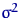 неизвестна. Критерий, который мы построим, тоже называют
критерием Стьюдента, только одновыборочным.
неизвестна. Критерий, который мы построим, тоже называют
критерием Стьюдента, только одновыборочным.
Введем функцию отклонения 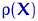 равную
равную
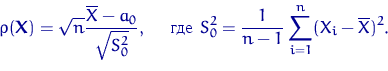
Сразу по п.4 следствия леммы Фишера имеем K1(a):
если 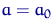 , то
, то 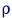 имеет распределение Стьюдента
имеет распределение Стьюдента 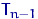 .
.
Упражнение. Доказать свойство
K1(б).
Критерий строится в точности как в (28),
но в качестве 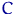 следует брать квантиль распределения Стьюдента, а не стандартного
нормального распределения. почему?
следует брать квантиль распределения Стьюдента, а не стандартного
нормального распределения. почему?
Упражнение. Нарисовать критерий и доказать,
что этот критерий имеет точный размер
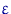
и является состоятельным.
Упражнение. В самом ли деле три последних
критерия состоятельны?
Напоминание. А вы доказали выполнение
свойства
K1(б) для функций отклонения этих критериев,
чтобы говорить о состоятельности?
А что такое «состоятельность» критерия?
N.I.Chernova
9 сентября 2002
![]() неизвестна. Критерий, который мы построим, тоже называют
критерием Стьюдента, только одновыборочным.
неизвестна. Критерий, который мы построим, тоже называют
критерием Стьюдента, только одновыборочным.
![]() равную
равную
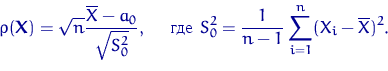
![]() , то
, то ![]() имеет распределение Стьюдента
имеет распределение Стьюдента ![]() .
.