Имеется выборка ![]() из нормального распределения
из нормального распределения
![]() с известной дисперсией
с известной дисперсией ![]() . Проверяется простая гипотеза
. Проверяется простая гипотеза ![]() против сложной
альтернативы
против сложной
альтернативы ![]() .
.
Построим критерий точного размера ![]() с помощью
функции отклонения
с помощью
функции отклонения ![]()
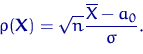
Очевидно свойство K1(a):
если ![]() верна, то
верна, то ![]() имеет стандартное нормальное распределение.
имеет стандартное нормальное распределение.
По ![]() выберем
выберем ![]() — квантиль
стандартного нормального распределения. Тогда
— квантиль
стандартного нормального распределения. Тогда
![]()
Критерий выглядит как все критерии согласия:
 | (28) |
N.I.Chernova