Совпадение дисперсий двух нормальных выборок

Есть две независимые выборки из нормальных распределений: ${\mathbf X}=(X_1, \ldots, X_n)$ из ${\mathsf N}_{a_1,\sigma_1^2}$ и ${\mathbf Y}=(Y_1,\ldots,Y_m)$ из ${\mathsf N}_{a_2,\sigma_2^2}$ , средние которых, вообще говоря, неизвестны. Критерий Фишера предназначен для проверки гипотезы $H_1=\{\sigma_1^2= \sigma_2^2\}$ .

Обозначим через $S_0^2({\mathbf X})$ и $S_0^2({\mathbf Y})$ несмещенные выборочные дисперсии:

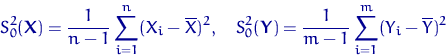
$\begin{displaymath} S_0^2({\mathbf X})=\dfrac{1}{n-1}\sum_{i=1}^n(X_i-\overline ... ...Y})=\dfrac{1}{m-1}\sum_{i=1}^m(Y_i-\overline Y)^2 \qquad \qquad\end{displaymath}$

и зададим функцию отклонения $\rho({\mathbf X},{\mathbf Y})$ как их отношение $\rho({\mathbf X},{\mathbf Y})=\dfrac{S_0^2({\mathbf X})}{S_0^2({\mathbf Y})}.$

Теорема 11.

Если гипотеза верна, то случайная величина $\rho({\mathbf X},{\mathbf Y})$ имеет распределение Фишера ${\mathsf F}_{n-1,m-1}$ с ${n{-}1,\,m{-}1}$ степенями свободы.

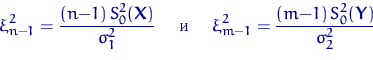
$\begin{displaymath} \xi^2_{n-1}=\dfrac{(n{-}1)\,S_0^2({\mathbf X})}{\sigma_1^2} ... ...d } \xi^2_{m-1}=\dfrac{(m{-}1)\,S_0^2({\mathbf Y})}{\sigma_2^2}\end{displaymath}$

имеют распределения ${\mathsf H}_{m-1}$ и ${\mathsf H}_{n-1}$ соответственно. При $\sigma_1^2=\sigma_2^2$ отношение

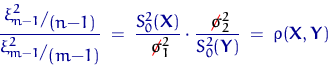
$\begin{displaymath} \dfrac{\raisebox{.3\height}{$\xi^2_{n{-}1}$}/\raisebox{-.3\h... ...gma_2^2}}{S_0^2({\mathbf Y})}\;=\;\rho({\mathbf X},{\mathbf Y})\end{displaymath}$

имеет распределение Фишера с ${n{-}1,\,m{-}1}$ степенями свободы по определению 18 и совпадает с $\rho({\mathbf X},{\mathbf Y})$ .

Упражнение. Доказать, что для любой альтернативы $\sigma_1^2\ne\sigma_2^2$

$\begin{equation} \rho({\mathbf X},{\mathbf Y})\; \buildrel {p} \over \longrighta... ... \dfrac{\sigma_1^2}{\sigma_2^2}\;\ne 1 \textrm{при } n,m\to\infty.\end{equation}$ при $n,m\to\infty$ . (27)

Построим критерий Фишера и убедимся, что (27) обеспечивает его состоятельность. Возьмем квантили $f_{\varepsilon/2}$ и $f_{1-\varepsilon/2}$ распределения Фишера ${\mathsf F}_{n-1,m-1}$ . Критерием Фишера называют критерий

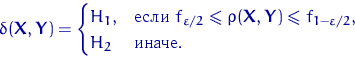
$\begin{displaymath} \delta({\mathbf X}, {\mathbf Y})=\begin{cases} H_1, & \text... ...t f_{1-\varepsilon/2}, \cr H_2 & \textrm{иначе. } \end{cases}\end{displaymath}$

Доказательство состоятельности критерия Фишера.

Покажем, что последовательность квантилей $f_\delta=f_\delta(n,m)$ любого уровня $0\,{<}\,\delta\,{<}\,1$ распределения ${\mathsf F}_{n,m}$ сходится к 1 при $n,m\,{\to}\,\infty$ .

Возьмем величину $f_{n,m}$ с этим распределением. По определению, ${\mathsf P}\,(f_{n,m}\,{<}\,f_\delta)=\delta$ , ${\mathsf P}\,(f_{n,m}\,{\gt}\,f_\delta)=1-\delta$ при всех

По свойству 2 распределения Фишера, $f_{n,m}\,{ \buildrel {p} \over \longrightarrow }\,1$ . Поэтому для любого $\epsilon\,{\gt}\,0$ обе вероятности ${\mathsf P}\,(f_{n,m}\,{<}\,1{-}\epsilon)$ и ${\mathsf P}\,(f_{n,m}\,{\gt}\,1{+}\epsilon)$ стремятся к нулю при $n,m\to\infty$ , становясь рано или поздно меньше как $\delta$ , так и $1{-}\delta$ .

Следовательно, при достаточно больших

выполнено $1-\epsilon<f_\delta<1+\epsilon$ .

Для доказательства состоятельности осталось предположить, что гипотеза

не верна, взять $\epsilon$ равное, например, половине расстояния от 1 до ${\sigma_1^2}/{\sigma_2^2}$ и использовать сходимость (27). Пусть, скажем, при достаточно больших

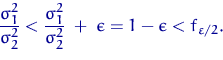
$\begin{displaymath} \dfrac{\sigma_1^2}{\sigma_2^2}< \dfrac{\sigma_1^2}{\sigma_2^2}\;+\;\epsilon= 1-\epsilon < f_{\varepsilon/2}.\end{displaymath}$

Тогда вероятность ошибки второго рода удовлетворяет неравенствам

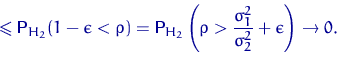
$\begin{displaymath} \alpha_2(\delta)={\mathsf P}\,\!_{H_2}(f_{\varepsilon/2}\leqslant \rho\leqslant f_{1-\varepsilon/2}) \end{displaymath}$ $\begin{displaymath} \leqslant {\mathsf P}\,\!_{H_2}(1-\epsilon<\rho)= {\mathsf ... ...eft(\rho\gt\dfrac{\sigma_1^2}{\sigma_2^2}+\epsilon\right)\to 0.\end{displaymath}$

Аналогично рассматривается случай, когда (при достаточно больших

)

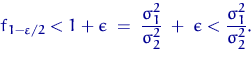
$\begin{displaymath} f_{1-\varepsilon/2}<1+\epsilon\;=\;\dfrac{\sigma_1^2}{\sigma_2^2}\;+\;\epsilon < \dfrac{\sigma_1^2}{\sigma_2^2}.\end{displaymath}$

Упражнение. Сформулировать критерий Фишера в случае, когда средние известны. Какой статистикой вы воспользуетесь теперь?

Критерий Фишера используют в качестве первого шага в задаче проверки однородности двух независимых нормальных выборок. Особенно часто возникает необходимость проверить равенство средних двух нормальных совокупностей -- например, в медицине или биологии для выяснения наличия или отсутствия действия препарата. Эта задача решается с помощью критерия Стьюдента (с ним мы познакомимся на следующей странице), но только в случае, когда неизвестные дисперсии равны. Для проверки этого предположения пользуются сначала критерием Фишера. Самое печальное, если гипотеза равенства дисперсий отвергается критерием Фишера, либо если сразу заведомо известно, что неизвестные дисперсии различны. Задачу о проверке равенства средних в этих условиях называют проблемой Беренса — Фишера. Ее решение возможно лишь в частных случаях, и больше о ней мы ничего говорить не будем.

8.6. Совпадение дисперсий двух нормальных выборок