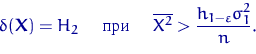Следующее замечательное утверждение, по недоразумению называемое леммой, заявляет, что оптимальные во всех трех смыслах (минимаксные, байесовские, наиболее мощные) критерии могут быть построены в самом общем случае простым выбором различных констант в одном и том же критерии — критерии отношения правдоподобия.
Пусть ![]() — выборка (набор независимых, одинаково
распределенных величин), и имеются две гипотезы о распределении
— выборка (набор независимых, одинаково
распределенных величин), и имеются две гипотезы о распределении ![]() :
:
![]()
Пусть ![]() — плотность распределения
— плотность распределения ![]() ,
,
![]() — плотность распределения
— плотность распределения ![]() , а
, а
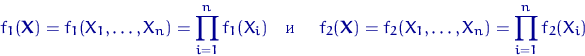
— соответствующие функции правдоподобия.
Если одно из распределений дискретно, а другое абсолютно непрерывно,
то всегда существует критерий с нулевыми вероятностями ошибок.
Смешанные распределения мы рассматривать не будем. Математики вместо этого
могут предполагать, что оба распределения абсолютно непрерывны относительно одной
и той же ![]() -конечной меры и имеют относительно нее плотности
-конечной меры и имеют относительно нее плотности ![]() и
и ![]() .
.
Мы будем выбирать гипотезу в зависимости от отношения функций правдоподобия. Напомним, что функция правдоподобия есть плотность распределения выборки.
Обратимся к примеру 30. Естественным кажется принимать вторую гипотезу,
если ![]() лежит правее точки пересечения плотностей
лежит правее точки пересечения плотностей ![]() . То есть
. То есть
там, где вторая плотность больше, принимать вторую гипотезу, там, где первая — первую.
Такой критерий сравнивает отношение
![]() с единицей, относя к критической области
ту часть
с единицей, относя к критической области
ту часть ![]() , где это отношение больше единицы. Заметим, что
при этом мы получим ровно один, не обязательно оптимальный, критерий
с некоторым фиксированным размером и мощностью.
, где это отношение больше единицы. Заметим, что
при этом мы получим ровно один, не обязательно оптимальный, критерий
с некоторым фиксированным размером и мощностью.
Если же нужно получить критерий c заранее заданным размером
![]() , либо иметь возможность варьировать и размер,
и мощность критерия, то следует рассмотреть класс похожих критериев, введя
свободный параметр:
, либо иметь возможность варьировать и размер,
и мощность критерия, то следует рассмотреть класс похожих критериев, введя
свободный параметр:
там, где вторая плотность в ![]() раз превосходит первую, выбирать вторую
гипотезу, иначе — первую,
раз превосходит первую, выбирать вторую
гипотезу, иначе — первую,
т.е. сравнивать отношение
плотностей ![]() не с единицей, а с некоторой
постоянной
не с единицей, а с некоторой
постоянной ![]() .
.
Назовем отношением правдоподобия частное
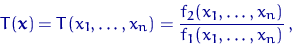 | (18) |
Конструкция критерия, который мы живописали выше, сильно усложнится
в случае, когда распределение случайной величины
![]() не является непрерывным, т.е. существует такое число
не является непрерывным, т.е. существует такое число ![]() , что вероятность
, что вероятность
![]() отлична от нуля. Это означает, что
на некотором «большом» множестве значений выборки обе гипотезы
«равноправны»: отношение правдоподобия постоянно. Относя это множество
целиком к критическому множеству или целиком исключая из него, мы
меняем вероятность ошибки первого рода (размер) критерия
на положительную величину
отлична от нуля. Это означает, что
на некотором «большом» множестве значений выборки обе гипотезы
«равноправны»: отношение правдоподобия постоянно. Относя это множество
целиком к критическому множеству или целиком исключая из него, мы
меняем вероятность ошибки первого рода (размер) критерия
на положительную величину ![]() :
:
![]()
И если вдруг мы захотим приравнять
вероятность ошибки первого рода к заранее выбранному числу ![]() , может случиться так, что критерий с критическим множеством
, может случиться так, что критерий с критическим множеством
![]() имеет размер больший, чем
имеет размер больший, чем ![]() , а критерий с критическим множеством
, а критерий с критическим множеством
![]() — размер меньший, чем
— размер меньший, чем ![]() .
.
Поэтому для математиков, не читающих [1],
мы сформулируем замечательно мощное утверждение мелким шрифтом,
зато в общем случае.
Затем для почти математиков сформулируем и докажем частный, но
наиболее частый случай, когда отношение правдоподобия
![]() имеет при верной первой гипотезе
непрерывную функцию распределения, т.е.
имеет при верной первой гипотезе
непрерывную функцию распределения, т.е. ![]() для любого
для любого ![]() .
.
Функция ![]() , принимающая значения
в интервале
, принимающая значения
в интервале ![]() в зависимости от значений выборки,
называется рандомизированным критерием.
в зависимости от значений выборки,
называется рандомизированным критерием.
Значение этой функции
трактуют как вероятность принять вторую (так удобнее) гипотезу
в некотором дополнительном эксперименте. Т.е., получив значение
![]() , мы должны дополнительно провести испытание
с вероятностью успеха
, мы должны дополнительно провести испытание
с вероятностью успеха ![]() , и в случае успеха принять
, и в случае успеха принять ![]() ,
в случае неудачи —
,
в случае неудачи — ![]() .
.
Значение ![]() предписывает
принять вторую гипотезу (с вероятностью 1, т.е. обязательно), а
значение
предписывает
принять вторую гипотезу (с вероятностью 1, т.е. обязательно), а
значение ![]() предписывает не принимать вторую гипотезу,
а принять первую.
предписывает не принимать вторую гипотезу,
а принять первую.
Напомним, что ![]() есть отношение правдоподобия, которое
мы ввели в (18).
есть отношение правдоподобия, которое
мы ввели в (18).
Размер и мощность КОП вычисляются по формуле полной вероятности. Размер равен
![]()
Мощность равна
![]()
Вероятность ошибки второго рода можно найти и иначе:
![]()
Существуют постоянные ![]() и
и ![]() , при которых
критерий отношения правдоподобия является
, при которых
критерий отношения правдоподобия является
![]()
Мы не ограничиваем значения ![]() областью
областью ![]() . Возможность брать
. Возможность брать ![]() (меньше бессмысленно, ибо
(меньше бессмысленно, ибо ![]() ) избавляет от ограничения
) избавляет от ограничения ![]() на возможный размер НМК. Это довольно сомнительное обобщение — ведь
уже критерий
на возможный размер НМК. Это довольно сомнительное обобщение — ведь
уже критерий ![]() имеет единичную мощность
при размере равном
имеет единичную мощность
при размере равном ![]() . Можно увеличивать размер
и дальше, но мощности расти уже некуда. Такой НМК будет
принимать с положительной вероятностью гипотезу
. Можно увеличивать размер
и дальше, но мощности расти уже некуда. Такой НМК будет
принимать с положительной вероятностью гипотезу ![]() там, где она верна
быть не может — в области
там, где она верна
быть не может — в области ![]() .
.
Всюду далее предполагается, что
Функция |
(19) |
Функция ![]() есть просто хвост функции распределения
случайной величины
есть просто хвост функции распределения
случайной величины ![]() :
:
![]()
Ее непрерывность означает, что
величина ![]() равна нулю для любого
равна нулю для любого ![]() . Это предположение избавляет нас от необходимости рассматривать рандомизированные
критерии. Итак,
. Это предположение избавляет нас от необходимости рассматривать рандомизированные
критерии. Итак,
Размер и вероятность ошибки второго рода этого критерия равны соответственно
![]()
Пусть
выполнено (19). Тогда существует постоянная ![]() , при которой
критерий отношения правдоподобия является
, при которой
критерий отношения правдоподобия является
Доказательство. Доказать достаточно два утверждения: существование постоянной ![]() ,
удовлетворяющей первому и третьему пунктам леммы, и оптимальность соответствующего
критерия. Начнем с третьего пункта.
,
удовлетворяющей первому и третьему пунктам леммы, и оптимальность соответствующего
критерия. Начнем с третьего пункта.
![]()
Итак, ![]() непрерывно меняется от
непрерывно меняется от ![]() до , поэтому
для любого
до , поэтому
для любого ![]() существует
существует ![]() такое,
что
такое,
что ![]() .
.
Функция ![]() , в отличие от
, в отличие от ![]() , не убывает по
, не убывает по ![]() . К тому же при
. К тому же при ![]() величина
величина
![]() стремится к
стремится к ![]() . Она тоже, подобно
. Она тоже, подобно ![]() , при
, при ![]() непрерывна по
непрерывна по ![]() из-за предположения (19):
из-за предположения (19):
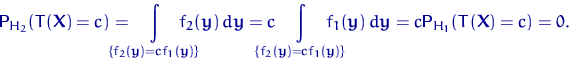
Поэтому функции ![]() и
и ![]() пересекаются
хотя бы однажды.
пересекаются
хотя бы однажды.
Действительно,
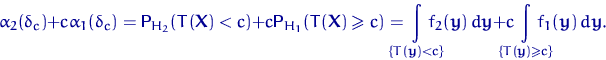
Но на множестве ![]() подынтегральная
функция
подынтегральная
функция ![]() совпадает с
совпадает с ![]() . И на
множестве
. И на
множестве ![]() подынтегральная
функция
подынтегральная
функция ![]() тоже совпадает с
тоже совпадает с ![]() . Продолжая
цепочку равенств, получим
. Продолжая
цепочку равенств, получим
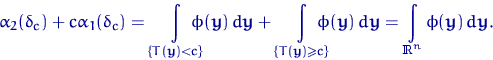
Q.D.E.
Пусть ![]() — любой другой критерий. Лемма 3 влечет странное
следствие:
— любой другой критерий. Лемма 3 влечет странное
следствие:
Каково бы ни было ![]() , вероятности ошибок любого критерия
, вероятности ошибок любого критерия ![]() связаны с вероятностями ошибок КОП
связаны с вероятностями ошибок КОП ![]() неравенством
неравенством
| (20) |
Доказательство.
Рассматривая для краткости нерандомизированный критерий ![]() ,
получим
,
получим
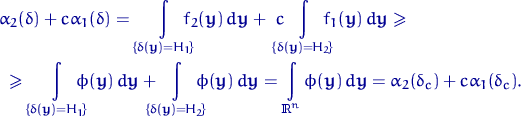
Q.D.E.
I. Пусть ![]() таково, что
таково, что
![]() .
Тогда правая часть неравенства (20) равна
.
Тогда правая часть неравенства (20) равна
![]() , и
для любого иного критерия
, и
для любого иного критерия ![]()
![]()
Итак, ![]() , т.е.
, т.е.
![]() — минимаксный.
— минимаксный.
II. Пусть ![]() и
и ![]() .
Тогда для любого иного критерия
.
Тогда для любого иного критерия ![]() неравенство (20) превращается в определение байесовского критерия:
неравенство (20) превращается в определение байесовского критерия:
![]()
Если же ![]() , то
, то ![]() . Тогда
КОП имеет нулевой размер и автоматически является байесовским.
. Тогда
КОП имеет нулевой размер и автоматически является байесовским.
III. Пусть ![]() таково, что
таково, что ![]() . Любой иной критерий
. Любой иной критерий ![]() из класса
из класса ![]() имеет размер
имеет размер
![]() . Используя в неравенстве (20)
оба этих размера, получим
. Используя в неравенстве (20)
оба этих размера, получим
![]()
Итак, ![]() , т.е.
, т.е.
![]() — НМК в классе
— НМК в классе ![]() .
.
Q.D.E.
Имеется выборка ![]() ,
, ![]() ,
, ![]() из нормального распределения
со средним
из нормального распределения
со средним ![]() и единичной дисперсией.
Построим минимаксный, байесовский для
и единичной дисперсией.
Построим минимаксный, байесовский для ![]() ,
, ![]() и наиболее мощный
размера
и наиболее мощный
размера ![]() критерии
для проверки гипотезы
критерии
для проверки гипотезы ![]() против
альтернативы
против
альтернативы ![]() , где
, где ![]() .
Отношение правдоподобия
имеет абсолютно непрерывное распределение при любой из гипотез, поэтому
критерий отношения правдоподобия 28
будет нерандомизированным, и достаточно описать только его критическую область
.
Отношение правдоподобия
имеет абсолютно непрерывное распределение при любой из гипотез, поэтому
критерий отношения правдоподобия 28
будет нерандомизированным, и достаточно описать только его критическую область
![]() .
Она определяется неравенством
.
Она определяется неравенством
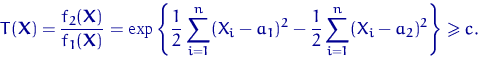 | (21) |
Критерий будет байесовским при ![]() .
Упростим неравенство (21). Получим
.
Упростим неравенство (21). Получим
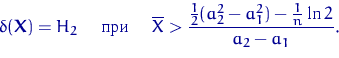
Например, при ![]() и
и ![]() критическая область имеет вид
критическая область имеет вид
![]() .
Чтобы построить минимаксный и наиболее мощный критерии, запишем
неравенство (21) в эквивалентном виде
.
Чтобы построить минимаксный и наиболее мощный критерии, запишем
неравенство (21) в эквивалентном виде ![]() , и искать будем
, и искать будем
![]() , а не
, а не ![]() . Размер и вероятность ошибки второго рода равны соответственно
. Размер и вероятность ошибки второго рода равны соответственно
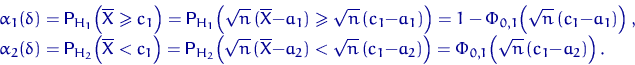
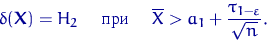
При ![]() получим минимаксный критерий. Пользуясь
свойствами функции распределения стандартного нормального закона, запишем
получим минимаксный критерий. Пользуясь
свойствами функции распределения стандартного нормального закона, запишем
![]()
откуда ![]() и
и ![]() . Минимаксный критерий имеет вид
. Минимаксный критерий имеет вид
![]()
Имеется выборка ![]() ,
, ![]() ,
, ![]() из нормального распределения
со средним и дисперсией
из нормального распределения
со средним и дисперсией ![]() ,
, ![]() .
Построим наиболее мощный критерий размера
.
Построим наиболее мощный критерий размера ![]() для проверки гипотезы
для проверки гипотезы ![]() против
альтернативы
против
альтернативы ![]() , где
, где ![]() .
Отношение правдоподобия снова
имеет абсолютно непрерывное распределение при любой из гипотез, поэтому
критерий отношения правдоподобия из определения 28
будет нерандомизированным. Его критическая область
.
Отношение правдоподобия снова
имеет абсолютно непрерывное распределение при любой из гипотез, поэтому
критерий отношения правдоподобия из определения 28
будет нерандомизированным. Его критическая область
![]() определяется неравенством
определяется неравенством
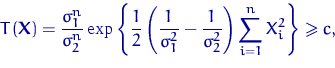
что эквивалентно неравенству ![]() . Найдем
. Найдем
![]() , при котором размер критерия равен
, при котором размер критерия равен ![]() :
:
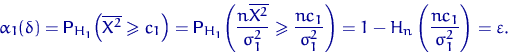
Отсюда ![]() , где
, где ![]() —
квантиль
—
квантиль ![]() -распределения с
-распределения с ![]() степенями свободы уровня
степенями свободы уровня ![]() . Тогда
. Тогда ![]() и НМК
размера
и НМК
размера ![]() имеет вид
имеет вид