Две простые гипотезы

Рассмотрим подробно случай, когда имеются две простые гипотезы о распределении наблюдений:

$\begin{displaymath} H_1=\bigl\{\mathscr F=\mathscr F_1\bigr\}, \quad H_2=\bigl\{\mathscr F=\mathscr F_2\bigr\}.\end{displaymath}$

Каков бы ни был критерий $\delta({\mathbf X})\,:\,{\textrm{\upshape I\kern-0.20em R}}^n\to\{H_1,H_2\}$ , он принимает не более двух значений. То есть область ${\textrm{\upshape I\kern-0.20em R}}^n$ делится на две части ${\textrm{\upshape I\kern-0.20em R}}^n=S\cup({\textrm{\upshape I\kern-0.20em R}}^n\backslash S)$ так, что

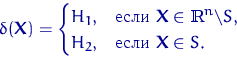
$\begin{displaymath} \delta({\mathbf X})=\begin{cases} H_1, & \textrm{если }{\mat... ...ash S, \cr H_2, & \textrm{если }{\mathbf X} \in S. \end{cases}\end{displaymath}$

Область

, в которой принимается вторая (альтернативная) гипотеза, называют критической областью.

Определение 22.

Вероятность ошибки первого рода $\alpha_1=\alpha_1(\delta)$ называют размером или уровнем значимости критерия $\delta$ :

$\begin{displaymath} \alpha_1=\alpha_1(\delta)={\mathsf P}\,{\!}_{H_1}(\delta({\m... ...a({\mathbf X})=H_2)= {\mathsf P}\,{\!}_{H_1}({\mathbf X}\in S).\end{displaymath}$

Мощностью критерия $\delta$ называют величину $1-\alpha_2$ , где $\alpha_2=\alpha_2(\delta)$ — вероятность ошибки второго рода критерия $\delta$ . Мощность критерия равна

$\begin{displaymath} 1-\alpha_2(\delta)=1-{\mathsf P}\,{\!}_{H_2}(\delta({\mathbf... ...({\mathbf X})= H_2)= {\mathsf P}\,{\!}_{H_2}({\mathbf X}\in S).\end{displaymath}$

Заметим, что вероятности ошибок первого и второго рода вычисляются при разных предположениях о распределении (если верна

и если верна

), так что никаких раз и навсегда фиксированных соотношений (например, $\alpha_1=1-\alpha_2$ , независимо от вида гипотез и вида критерия) между ними нет. Рассмотрим крайний случай, когда критерий, независимо от выборки, всегда принимает одну и ту же гипотезу.

Пример 29.

Имеются гипотезы , и критерий $\delta({\mathbf X})\equiv H_1$ , то есть пусто. Тогда

$\alpha_1={\mathsf P}\,{\!}_{H_1}(\textrm{принять }~H_2)=0$ , $\alpha_2={\mathsf P}\,{\!}_{H_2}(\textrm{принять }~H_1)=1$ .

Наоборот: пусть имеются гипотезы , и критерий $\delta({\mathbf X})\equiv H_2$ , то есть $S={\textrm{\upshape I\kern-0.20em R}}^n$ . Тогда

$\alpha_1={\mathsf P}\,{\!}_{H_1}(\textrm{принять }~H_2)=1$ , $\alpha_2={\mathsf P}\,{\!}_{H_2}(\textrm{принять }~H_1)=0$ .

Примеры 29 и 30 показывают общую тенденцию: при попытке уменьшить одну из вероятностей ошибок критерия другая, как правило, увеличивается. Так, если уменьшать $\alpha_1={\mathsf P}\,{\!}_{H_1}({\mathbf X}\in S)$ мы будем, сужая критическую область

, то одновременно будет уменьшаться мощность критерия $1-\alpha_2={\mathsf P}\,{\!}_{H_2}({\mathbf X}\in S)$ .

Пример 30.

Имеется выборка объема 1 из нормального распределения ${\mathsf N}_{a,1}$ и две простые гипотезы о среднем: $H_1=\{a=0\}$ и $H_2=\{a=1\}$ . Рассмотрим следующий критерий (при некотором вещественном ):

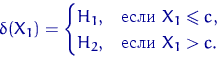
$\begin{displaymath} \delta(X_1)=\begin{cases} H_1, & \textrm{если }X_1 \leqslant c, \cr H_2, & \textrm{если }X_1 \gt c. \end{cases}\end{displaymath}$

Изобразим на графике соответствующие гипотезам плотности и вероятности ошибок первого и второго рода критерия $\delta$ :

$\begin{displaymath} \alpha_1={\mathsf P}\,{\!}_{H_1}(\delta(X_1) = H_2)={\mathsf... ...2}(\delta(X_1) = H_1)={\mathsf P}\,{\!}_{H_2}(X_1 \leqslant c).\end{displaymath}$

Рис. 8: Две простые гипотезы.

$\begin{figure} \begin{center} \unitlength=1mm \begin{picture} (101,16) \linethi... ...,2){\makebox(0,0)[rb]{{\small $\alpha_1$}}}\end{picture}\end{center}\end{figure}$

**Рис. 8:** Две простые гипотезы.
$\begin{figure} \begin{center} \unitlength=1mm \begin{picture} (101,16) \linethi... ...,2){\makebox(0,0)[rb]{{\small $\alpha_1$}}}\end{picture}\end{center}\end{figure}$

Видим, что с ростом вероятность ошибки первого рода $\alpha_1$ уменьшается, но вероятность ошибки второго рода $\alpha_2$ растет.

Итак, критерий тем лучше, чем меньше вероятности его ошибок. Но сравнивать критерии по паре вероятностей ошибок

$\begin{displaymath} \alpha_i(\delta_1)\leqslant \alpha_i(\delta_2) \quad \textrm{ при }\quad i=1,2,\end{displaymath}$

7.1. Две простые гипотезы