next up previous index
Next:  BLUE   Up:  Эффективные оценки   Previous:  Неравенство Рао — Крамера

4.4.   Неравенство Рао — Крамера и эффективность оценок

Сформулируем очевидное следствие из неравенства Рао — Крамера.

Следствие 1.

  Если семейство распределений $\mathscr F_\theta$ удовлетворяет условиям регулярности (R) и (RR), и оценка $\theta^*\in K_{b(\theta)}$ такова, что в неравенстве Рао — Крамера достигается равенство:

\begin{displaymath} {\mathsf E}_\theta\,\left(\theta^*-\theta\right)^2 = \dfrac{... ...sf D}_\theta\,\theta^* = \dfrac{(1+b'(\theta))^2}{n I(\theta)},\end{displaymath}

то оценка $\theta^*$ эффективна в классе $K_{b(\theta)}$.

Оценку, для которой в неравенстве Рао — Крамера достигается равенство, иногда называют $R$-эффективной оценкой. Следствие 1 можно сформулировать так:

Следствие 1.  Eсли оценка $R$-эффективна в некотором классе, то она эффективна в этом классе.
.

Пример 18.

Для выборки $X_1$, $\ldots$, $X_n$ из распределения Бернулли ${\mathsf B}_p$ несмещенная оценка $p^*=\overline X$ эффективна, так как для нее достигается равенство в неравенстве Рао — Крамера (см. [3, пример 13.20, с.67]).

Пример 19.

Пусть $X_1$, $\ldots$, $X_n$ — выборка объема $n$ из нормального распределения ${\mathsf N}_{a,\sigma^2}$, где $a\in {\textrm{\upshape I\kern-0.20em R}}$, $\sigma\gt$. Проверим, является ли оценка $a^*=\overline X\in K_0$ эффективной (см. также [3, пример 13.6, с.64]).

Найдем информацию Фишера относительно параметра $a$ (считая, что имеется один неизвестный параметр — $a$).

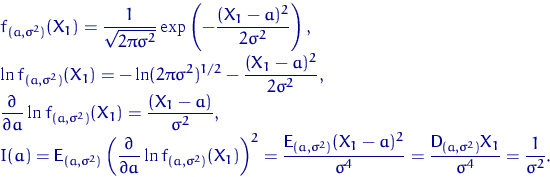
\begin{eqnarray*} && f_{(a,\sigma^2)}(X_1) = \dfrac{1}{\sqrt{2\pi\sigma^2}} \ex... ...thsf D}\,{\!}_{(a,\sigma^2)}X_1}{\sigma^4}= \dfrac{1}{\sigma^2}.\end{eqnarray*}

Итак, $I(a)=1/\sigma^2$. Найдем дисперсию оценки $\overline X$.

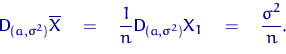
\begin{displaymath} {\mathsf D}\,{\!}_{(a,\sigma^2)}\overline X \quad = \quad \d... ... D}\,{\!}_{(a,\sigma^2)} X_1 \quad = \quad \dfrac{\sigma^2}{n}.\end{displaymath}

Далее, сравнивая левую и правую части в неравенстве Рао — Крамера, получаем равенство:

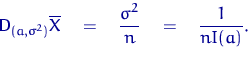
\begin{displaymath} {\mathsf D}\,{\!}_{(a,\sigma^2)}\overline X \quad = \quad \dfrac{\sigma^2}{n} \quad = \quad \dfrac{1}{n I(a)}.\end{displaymath}

То есть оценка $a^*=\overline X$ эффективна (обладает наименьшей дисперсией среди несмещенных оценок).

Пример 20.

Пусть $X_1$, $\ldots$, $X_n$ — выборка объема $n$ из нормального распределения ${\mathsf N}_{0,\sigma^2}$, где $\sigma\gt$. Проверим, является ли оценка ${\sigma^2}^*=\dfrac{1}{n}\sum\limits_{i=1}^n X_i^2=\overline{X^2}\in K_0$ эффективной.

Упражнение.    Получить эту оценку методом моментов и методом максимального правдоподобия.

Найдем информацию Фишера относительно параметра $\sigma^2$.

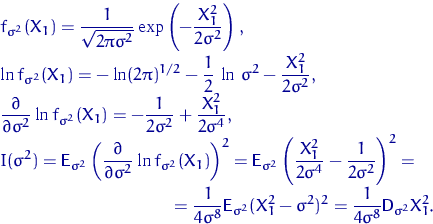
\begin{eqnarray*} && f_{\sigma^2}(X_1) = \dfrac{1}{\sqrt{2\pi\sigma^2}} \exp\le... ...ma^2)^2= \dfrac{1}{4\sigma^8} {\mathsf D}\,{\!}_{\sigma^2}X_1^2.\end{eqnarray*}

Осталось найти ${\mathsf D}\,{\!}_{\sigma^2}X_1^2={\mathsf E}\,{\!}_{\sigma^2}X_1^4-({\mathsf E}\,{\!}_{\sigma^2}X_1^2)^2= {\mathsf E}\,{\!}_{\sigma^2}X_1^4-\sigma^4$. Для тех, кто помнит некоторые формулы вероятности: величина $\xi=X_1/\sigma$ имеет стандартное нормальное распределение, и для нее

\begin{displaymath} {\mathsf E}\,\xi^{2k}=(2k-1)!!=(2k-1)(2k-3)\cdot\ldots\cdot 3\cdot 1,\end{displaymath}

Тогда $X_1=\xi\cdot\sigma$ и

\begin{displaymath} {\mathsf E}\,{\!} X_1^4={\mathsf E}\,\xi^4\cdot\sigma^4=3\sigma^4.\end{displaymath}

Те, кто не помнит, считаем заново:

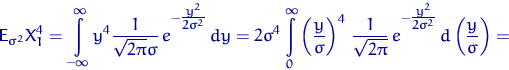
\begin{displaymath} {\mathsf E}\,{\!}_{\sigma^2}X_1^4=\int\limits_{-\infty}^{\in... ...e}^{-\tfrac{y^2}{2\sigma^2}}\,d\left(\dfrac{y}{\sigma} \right)=\end{displaymath}

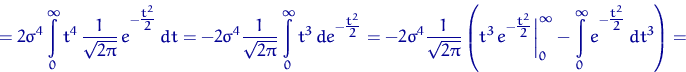
\begin{displaymath} =2\sigma^4\int\limits_{0}^{\infty} t^4\, {\frac{1}{\sqrt{2\p... ...ty} {\vphantom{\frac{1}{1}} e}^{-\tfrac{t^2}{2}}\,dt^3 \right)=\end{displaymath}

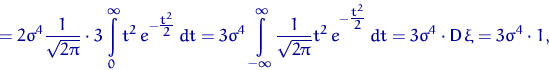
\begin{displaymath} =2\sigma^4 \dfrac{1}{\sqrt{2\pi}}\cdot 3 \int\limits_{0}^{\i... ...}{2}}\,dt = 3\sigma^4 \cdot {\mathsf D}\,\xi=3\sigma^4 \cdot 1,\end{displaymath}

где $\xi$ имеет стандартное нормальное распределение.

Итак, ${\mathsf D}\,{\!}_{\sigma^2}X_1^2={\mathsf E}\,{\!}_{\sigma^2}X_1^4-\sigma^4 = 2\sigma^4$,

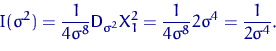
\begin{displaymath} I(\sigma^2)=\dfrac{1}{4\sigma^8} {\mathsf D}\,{\!}_{\sigma^2}X_1^2= \dfrac{1}{4\sigma^8} 2\sigma^4 = \dfrac{1}{2\sigma^4}.\end{displaymath}

Найдем дисперсию оценки ${\sigma^2}^*=\overline{X^2}$.

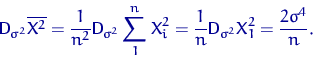
\begin{displaymath} {\mathsf D}\,{\!}_{\sigma^2} \overline{X^2} = \dfrac{1}{n^2}... ...}{n} {\mathsf D}\,{\!}_{\sigma^2} X_1^2 = \dfrac{2\sigma^4}{n}.\end{displaymath}

Сравнивая левую и правую части в неравенстве Рао — Крамера, получаем равенство:

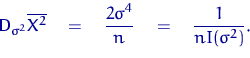
\begin{displaymath} {\mathsf D}\,{\!}_{\sigma^2}\overline{X^2} \quad = \quad \dfrac{2\sigma^4}{n} \quad = \quad \dfrac{1}{n I(\sigma^2)}.\end{displaymath}

Таким образом, оценка ${\sigma^2}^*=\overline{X^2}$ эффективна.

Упражнение.    Пусть $X_1$, $\ldots$, $X_n$ — выборка объема $n$ из нормального распределения ${\mathsf N}_{a,\sigma^2}$, где $a$ известно, $\sigma\gt$. Проверить, является ли эффективной оценка ${\sigma^2}^*=\dfrac{1}{n}\sum\limits_{i=1}^n (X_i-a)^2=\overline{(X-a)^2}$. Принадлежит ли эта оценка классу $K_0$? Какими методами получена? Является ли состоятельной и асимптотически нормальной?

Пример 21.

Пусть $X_1$, $\ldots$, $X_n$ — выборка объема $n$ из показательного распределения ${\mathsf E}\,{\!}_{1/\alpha}$ с параметром $1/\alpha$, где $\alpha\gt$. Проверим, является ли оценка $\alpha^*=\overline X\in K_0$ (оценка для параметра $\alpha$!) эффективной.

Найдем информацию Фишера относительно параметра $\alpha$

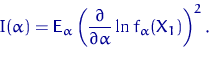
\begin{displaymath} I(\alpha)={\mathsf E}\,{\!}_\alpha\left(\dfrac{\partial}{\partial \alpha} \ln f_\alpha(X_1)\right)^2.\end{displaymath}

Плотность данного показательного распределения имеет вид:

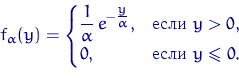
\begin{displaymath} f_\alpha(y)=\begin{cases} \dfrac{1}{\alpha}\,e^{-\tfrac{y}{\... ...m{если } y\gt,\cr 0, & \textrm{если } y\leqslant 0.\end{cases}\end{displaymath}

Тогда

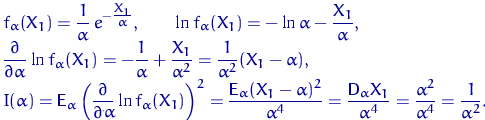
\begin{eqnarray*} && f_\alpha(X_1) = \dfrac{1}{\alpha}\,e... ...ha^4}= \dfrac{\alpha^2}{\alpha^4}= \dfrac{1}{\alpha^2}. \qquad \end{eqnarray*}

Итак, $I(\alpha)=1/\alpha^2$. Найдем дисперсию оценки $\overline X$.

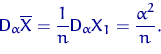
\begin{displaymath} {\mathsf D}\,{\!}_\alpha \overline X = \frac{1}{n} {\mathsf D}\,{\!}_\alpha X_1 = \frac{\alpha^2}{n}.\end{displaymath}

Подставив дисперсию и информацию Фишера в неравенство Рао — Крамера, получаем равенство:

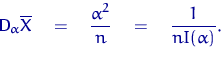
\begin{displaymath} {\mathsf D}\,{\!}_\alpha \overline X \quad = \quad \dfrac{\alpha^2}{n} \quad = \quad \frac{1}{n I(\alpha)}.\end{displaymath}

То есть оценка $\alpha^*=\overline X$ — эффективная оценка параметра $\alpha$.

Упражнение.    Получить эту оценку методом моментов и методом максимального правдоподобия. Она действительно несмещенная? А еще какими свойствами обладает?

Упражнение.    Проверьте, что для несмещенной оценки $\alpha^{**}=X_1$ равенство в неравенстве Рао — Крамера не достигается. Объясните, почему, исходя только из этого, нельзя сделать вывод о ее неэффективности в классе $K_0$. Сделайте этот вывод на основании того, что оценки $\alpha^*=\overline X$ и $\alpha^{**}=X_1$ принадлежат классу оценок с одинаковым смещением, и одна из них эффективна. Используйте теорему 5.

Отсутствие равенства в неравенстве Рао — Крамера вовсе не означает неэффективность оценки. Приведем пример оценки, которая является эффективной, но для которой не достигается равенство в неравенстве Рао — Крамера. В эффективности оценки из этого примера мы хотели бы, но не сможем убедиться.

Пример 22.

Пусть $X_1$, $\ldots$, $X_n$ — выборка объема $n$ из показательного распределения ${\mathsf E}\,{\!}_\alpha$ с параметром $\alpha$, где $\alpha\gt$. Возьмем чуть поправленную оценку метода моментов

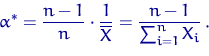
\begin{displaymath} \alpha^*=\dfrac{n-1}{n}\cdot\dfrac{1}{\overline X}=\dfrac{n-1}{\sum_{i=1}^n X_i}\,.\end{displaymath}

Убедимся, что это — несмещенная оценка. Согласно свойству устойчивости по суммированию для $\text{\boldmath\ensuremath \Gamma}$-распределения, сумма $\sum\limits_{i=1}^n X_i$ случайных величин с распределением ${\mathsf E}\,{\!}_{\alpha}=\text{\boldmath\ensuremath \Gamma}_{\alpha,1}$ имеет распределение $\text{\boldmath\ensuremath \Gamma}_{\alpha,n}$ с плотностью

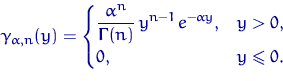
\begin{displaymath} \gamma_{\alpha,n}(y)=\begin{cases} \dfrac{\alpha^n}{\text{\b... ...-1}\,e^{-\alpha y}, & y\gt, \cr 0, & y\leqslant 0. \end{cases} \end{displaymath}

Напомним, что $\text{\boldmath\ensuremath \Gamma}(n)=(n-1)!$  Вычислим математическое ожидание

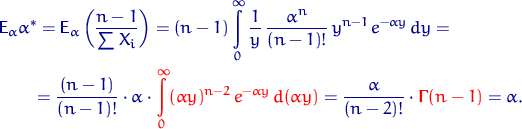
\begin{multline*} {\mathsf E}\,{\!}_{\alpha}\alpha^*={\mathsf E}\,{\!}_{\alpha}\... ... { \color {red} \text{\boldmath\ensuremath \Gamma}(n-1)}=\alpha.\end{multline*}

Итак, оценка $\alpha^*$ принадлежит классу $K_0$. Найдем информацию Фишера относительно параметра $\alpha$:

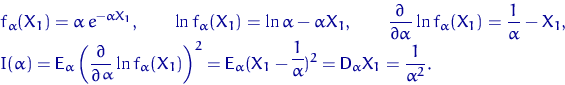
\begin{eqnarray*} && f_\alpha(X_1) = \alpha\,e^{-\alpha X_1}, \quad \quad \ln f_... ...X_1-\alpha)^2={\mathsf D}\,{\!}_\alpha X_1= \dfrac{1}{\alpha^2}.\end{eqnarray*}

Итак, $I(\alpha)=1/\alpha^2$. Найдем второй момент и дисперсию оценки $\alpha^*$.

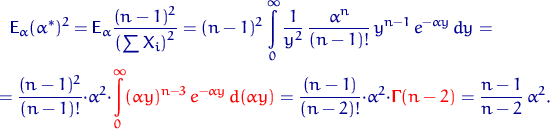
\begin{multline*} {\mathsf E}\,{\!}_{\alpha}(\alpha^*)^2={\mathsf E}\,{\!}_{\alp... ...xt{\boldmath\ensuremath \Gamma}(n-2)}=\dfrac{n-1}{n-2}\,\alpha^2.\end{multline*}

Тогда

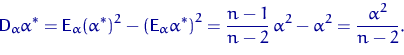
\begin{displaymath} {\mathsf D}\,{\!}_\alpha \alpha^* = {\mathsf E}\,{\!}_{\alph... ...)^2= \dfrac{n-1}{n-2}\,\alpha^2-\alpha^2=\dfrac{\alpha^2}{n-2}.\end{displaymath}

Подставив дисперсию и информацию Фишера в неравенство Рао — Крамера, получаем, что при любом $n$ есть строгое неравенство:

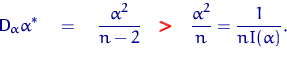
\begin{displaymath} {\mathsf D}\,{\!}_\alpha \alpha^* \quad = \quad \dfrac{\alph... ...} \pmb \gt} \quad\dfrac{\alpha^2}{n} = \frac{1}{n I(\alpha)}.\end{displaymath}

Тем не менее, оценка $\alpha^*$ является эффективной, но доказывать мы это не будем.


N.I.Chernova
9 сентября 2002