next up previous index
Next:  Неравенство Рао — Крамера   Up:  Эффективные оценки   Previous:  «Регулярные» и «нерегулярные» семейства

4.3.   Неравенство Рао — Крамера

Пусть $X_1$, $\ldots$, $X_n$ — выборка объема $n$ из параметрического семейства распределений $\mathscr F_\theta$, $\theta \in \Theta$, и семейство $\mathscr F_\theta$ удовлетворяет условию регулярности (R).

Пусть, кроме того, выполнено условие

(RR) «Информация Фишера»    $\displaystyle I(\theta) = {\mathsf E}_\theta\,\left(\dfrac{\partial}{\partial\theta} \ln {f_{\theta}(X_1)} \right)^2$ существует, положительна и непрерывна по $\theta$ во всех точках $\theta \in \Theta$.

Справедливо следующее утверждение.

Неравенство Рао — Крамера.

Пусть семейство распределений $\mathscr F_\theta$ удовлетворяет условиям (R) и (RR). Тогда для любой несмещенной оценки $\theta^*\in K_0$, дисперсия которой ${\mathsf D}_\theta\,\theta^*$ ограничена на любом компакте в области $\Theta$, справедливо неравенство

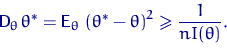
\begin{displaymath} {\mathsf D}_\theta\,\theta^*={\mathsf E}_\theta\,\left(\theta^*-\theta\right)^2 \geqslant \dfrac{1}{n I(\theta)}.\end{displaymath}

Упражнение.    Проверить, что для показательного семейства распределений ${\mathsf E}\,{\!}_\alpha$ с параметром $\alpha\gt$ дисперсия ${\mathsf D}\,{\!}_\alpha X_1$ не ограничена глобально при $\alpha\gt$, но ограничена на компактах.

Неравенство сформулировано для класса несмещенных оценок. В классе оценок с произвольным смещением $b(\theta)$ неравенство Рао — Крамера выглядит так:

Неравенство Рао — Крамера.

Пусть семейство распределений $\mathscr F_\theta$ удовлетворяет условиям (R) и (RR). Тогда для любой оценки $\theta^*\in K_{b(\theta)}$, дисперсия которой ${\mathsf D}_\theta\,\theta^*$ ограничена на любом компакте в области $\Theta$, справедливо неравенство

\begin{displaymath} {\mathsf E}_\theta\,\left(\theta^*-\theta\right)^2 \geqslant... ...heta\,\theta^* \geqslant \dfrac{(1+b'(\theta))^2}{n I(\theta)}.\end{displaymath}

Для доказательства нам понадобится следующее утверждение.

Лемма 2.

При выполнении условий (R) и (RR) для любой статистики $T=T({\mathbf X})$, дисперсия которой ограничена на компактах, имеет место равенство

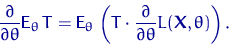
\begin{displaymath} \frac{\partial}{\partial\theta} {\mathsf E}_\theta\, T = {\m... ...t \frac{\partial}{\partial\theta}L({\mathbf X}, \theta)\right).\end{displaymath}

Упражнение.   Вспомнить, что такое функция правдоподобия $f({\mathbf X}, \theta)$, логарифмическая функция правдоподобия $L({\mathbf X}, \theta)$ (определение 6), как они связаны друг с другом, с плотностью $X_1$ и совместной плотностью выборки.

Доказательство леммы 2.

Напоминание: математическое ожидание функции от нескольких случайных величин есть (многомерный) интеграл от этой функции, помноженной на совместную плотность этих случайных величин.

Поэтому

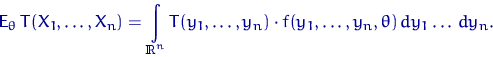
\begin{displaymath} {\mathsf E}_\theta\, T(X_1, \ldots, X_n) = \int\limits_{{\te... ...\ldots, y_n) \cdot f(y_1,\ldots,y_n, \theta)\,dy_1\ldots\,dy_n.\end{displaymath}

В следующей цепочке равенство, помеченное ($*$), мы доказывать не будем, поскольку его доказательство требует знания условий дифференцируемости интеграла по параметру (тема, выходящая за пределы курса МА на ЭФ). Это равенство — смена порядка дифференцирования и интегрирования — то единственное, ради чего введены условия регулярности (см. пример ниже).

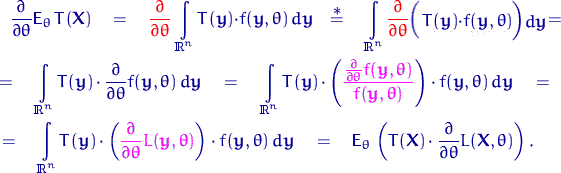
\begin{multline*} \frac{\partial}{\partial\theta} {\mathsf E}_\theta\, T({\mathb... ...dot \frac{\partial}{\partial\theta}L({\mathbf X}, \theta)\right).\end{multline*}

Через ${\mathbf y}$ в интегралах обозначен вектор $(y_1,\ldots,y_n)$.

Q.D.E.



Доказательство неравенства Рао — Крамера.  Мы докажем только неравенство для класса $K_0$. Необходимые изменения в доказательстве для класса $K_b$ читатель может внести самостоятельно.

Воспользуемся леммой 2. Будем брать в качестве $T({\mathbf X})$ разные функции и получать забавные формулы, которые потом соберем вместе.

1.
Пусть $T({\mathbf X})\equiv 1$. Тогда

\begin{displaymath} 0 = \dfrac{\partial}{\partial\theta} 1 = {\mathsf E}_\theta\, \dfrac{\partial}{\partial\theta}L({\mathbf X}, \theta).\end{displaymath}

Далее, поскольку $f({\mathbf X},\theta)=\prod f_\theta(X_i)$, то $L({\mathbf X}, \theta)=\displaystyle\sum \ln f_\theta(X_i)$, и

\begin{equation} { \color {red} 0}={\mathsf E}_\theta\, \dfrac{\partial}{\parti... ...= n \cdot { \color {red} {\mathsf E}_\theta\, \ln f_\theta(X_1)}.\end{equation}(10)

2.
Пусть $T({\mathbf X}) = \theta^*\in K_0$, т.е. ${\mathsf E}_\theta\, \theta^* = \theta$. Тогда

\begin{equation} \dfrac{\partial}{\partial\theta} {\mathsf E}_\theta\, \theta^* ... ...ta^* \cdot \dfrac{\partial}{\partial\theta}L({\mathbf X}, \theta).\end{equation}(11)

Вспомним свойство коэффициента корреляции:

\begin{displaymath} \mathrm{cov}(\xi,\eta) = {\mathsf E}\,\xi\eta-{\mathsf E}\,\... ...thsf E}\,\eta\leqslant\sqrt{{\mathsf D}\,\xi{\mathsf D}\,\eta}.\end{displaymath}

Используя свойства (10) и (11), имеем

\begin{displaymath} \mathrm{cov}\left(\theta^*, \dfrac{\partial}{\partial\theta... ...\theta\,\dfrac{\partial}{\partial\theta}L({\mathbf X}, \theta)=\end{displaymath}


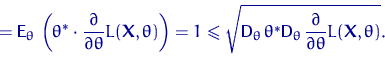\begin{equation} ={\mathsf E}_\theta\,\left(\theta^* \cdot \dfrac{\partial}{\pa... ...D}_\theta\,\frac{\partial}{\partial\theta}L({\mathbf X}, \theta)}.\end{equation}(12)

Найдем ${\mathsf D}_\theta\,\dfrac{\partial}{\partial\theta}L({\mathbf X}, \theta)$:

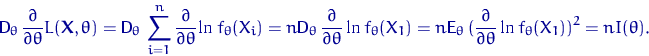
\begin{displaymath} {\mathsf D}_\theta\,\dfrac{\partial}{\partial\theta}L({\math... ...rac{\partial}{\partial\theta}\ln f_\theta(X_1))^2= n I(\theta).\end{displaymath}

Подставляя дисперсию в неравенство (12), получим

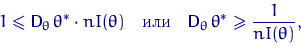
\begin{displaymath} 1\leqslant {\mathsf D}_\theta\,\theta^* \cdot n I(\theta) \q... ...d {\mathsf D}_\theta\,\theta^* \geqslant \frac{1}{n I(\theta)},\end{displaymath}

что и требовалось доказать.

Q.D.E.


Следующий пример показывает, что условие регулярности является существенным для выполнения равенства, помеченного ($*$) в лемме 2.


Пример 17   (нерегулярное семейство).

Рассмотрим равномерное распределение ${\mathsf U}_{0,\theta}$ с параметром $\theta\gt$. Выпишем при $n=1$ какой-нибудь интеграл и сравним производную от него и интеграл от производной: скажем, для $T(X_1)=1$

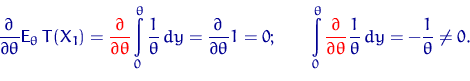
\begin{displaymath} \frac{\partial}{\partial\theta}{\mathsf E}_\theta\, T(X_1)= ... ...rtial\theta}} \frac{1}{\theta}\,dy = - \dfrac{1}{\theta}\neq 0.\end{displaymath}

Заметим, что и само утверждение неравенства Рао — Крамера для данного семейства распределений не выполнено: найдется оценка, дисперсия которой ведет себя как $1/n^2$, а не как $1/n$ в неравенстве Рао — Крамера.

Упражнение.      Проверить, что в качестве этой «выдающейся» из неравенства Рао — Крамера оценки можно брать, скажем, смещенную оценку $X_{(n)}$ или несмещенную оценку $\dfrac{n+1}{n} X_{(n)}\in K_0$.

N.I.Chernova
9 сентября 2002