В примере 12 мы видели, что для оценок типа ![]() свойство асимптотической нормальности сразу следует из ЦПТ.
свойство асимптотической нормальности сразу следует из ЦПТ.
Установим асимптотическую нормальность оценок более сложного вида, какими обычно оказываются оценки метода моментов.
Пусть функция ![]() такова, что
такова, что ![]() . Тогда статистика
. Тогда статистика ![]() является асимптотически нормальной оценкой для
является асимптотически нормальной оценкой для ![]() с коэффициентом
с коэффициентом ![]() :
:
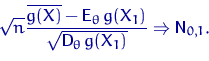
Следующая теорема утверждает асимптотическую нормальность оценок вида
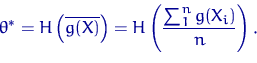
Такие оценки получаются обычно найти примеры! при использовании метода
моментов, при этом всегда ![]() .
.
Пусть функция ![]() такова, что
такова, что ![]() , а
функция
, а
функция ![]() непрерывно дифференцируема в точке
непрерывно дифференцируема в точке ![]() и
и ![]() .
.
Тогда оценка ![]() является асимптотически нормальной оценкой
для параметра
является асимптотически нормальной оценкой
для параметра ![]() с коэффициентом
с коэффициентом ![]() .
.
Доказательство теоремы 7. Согласно ЗБЧ последовательность ![]() стремится к
стремится к ![]() по вероятности
с ростом
по вероятности
с ростом ![]() . Функция
. Функция
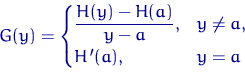
по условию непрерывна в точке ![]() . Поскольку сходимость
по вероятности сохраняется под действием непрерывной функции,
получим, что
. Поскольку сходимость
по вероятности сохраняется под действием непрерывной функции,
получим, что ![]() .
.
Заметим также, что по свойству 5
величина ![]() слабо сходится к нормальному распределению
слабо сходится к нормальному распределению ![]() .
Пусть
.
Пусть ![]() — случайная величина из этого распределения. Тогда
— случайная величина из этого распределения. Тогда

| |
 | |
 | |
Мы использовали свойство слабой сходимости:
если ![]() и
и ![]() , то
, то
![]() .
.
Но ![]() как раз и имеет распределение
как раз и имеет распределение ![]() .
.
Q.D.E.
Пусть ![]() ,
, ![]() ,
, ![]() — выборка объема
— выборка объема ![]() из равномерного распределения
из равномерного распределения ![]() , где
, где
![]() . Проверим, являются ли оценки
. Проверим, являются ли оценки
![]() ,
,
![]() =1, 2,..., полученные методом моментов в примере 4, асимптотически
нормальными.
=1, 2,..., полученные методом моментов в примере 4, асимптотически
нормальными.
Пусть ![]() ,
, ![]() . Тогда
. Тогда
![\begin{displaymath}
\theta^*_k=\sqrt[k]{(k+1)\overline{X^k}} = \sqrt[k]{\dfrac{\sum (k+1)X_i^k}{n}} =
H\left(\dfrac{\sum g(X_i)}{n}\right).\end{displaymath}](img518.gif)
При этом
![\begin{displaymath}
\theta=H\left({\mathsf E}_\theta\, g(X_1)\right)=\sqrt[k]{{\...
...}_\theta\, (k+1)X_1^k}=
\sqrt[k]{ (k+1)~\dfrac{\theta^k}{k+1}}.\end{displaymath}](img519.gif)
Впрочем, иначе быть не могло по определению метода моментов. верно? Проверим другие условия теоремы 7:
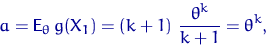
Дисперсия
![]()
конечна и отлична от нуля.
Функция ![]() непрерывно дифференцируема в точке
непрерывно дифференцируема в точке ![]() :
:
![]()
По теореме 7, оценка ![]() — АНО для
— АНО для ![]() с коэффициентом
с коэффициентом
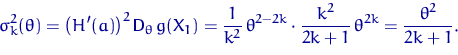
В том числе для ![]() имеем коэффициент
имеем коэффициент
![]() (см. пример 12).
(см. пример 12).
Осталось понять, при чем тут сравнение оценок и что показывает коэффициент асимптотической нормальности.
N.I.Chernova