next up previous index
Next:  Состоятельность оценок метода моментов   Up:  Точечное оценивание   Previous:  Точечные оценки. Несмещенность, состоятельность

2.3.   Методы нахождения оценок: метод моментов

Метод моментов заключается в следующем: любой момент случайной величины $X_1$ (например, $k$-й) зависит, часто функционально, от параметра $\theta$. Но тогда и параметр $\theta$ может оказаться функцией от теоретического $k$-го момента. Подставив в эту функцию вместо неизвестного теоретического $k$-го момента его выборочный аналог, получим вместо параметра $\theta$ оценку $\theta^*$.   Пусть $X_1$, $\ldots$, $X_n$ — выборка объема $n$ из параметрического семейства распределений $\mathscr F_\theta$, где $\theta \in \Theta$. Выберем некоторую функцию $g(y)$ так, чтобы существовал момент

\begin{equation} {\mathsf E}_\theta\, g(X_1) = h(\theta),\end{equation}(3)

и функция $h$ была обратима в области $\Theta$. Тогда в качестве оценки $\theta^*$ для $\theta$ возьмем решение уравнения

\begin{displaymath} \overline {g(X)} = h(\theta^*).\end{displaymath}

  Или (что то же самое), сначала решаем уравнение (3) относительно $\theta$, а затем вместо истинного момента берем выборочный:

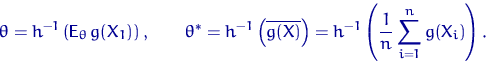
\begin{displaymath} \theta=h^{-1}\left({\mathsf E}_\theta\, g(X_1)\right), \qqua... ...X)}\right)= h^{-1}\left(\dfrac{1}{n}\sum_{i=1}^n g(X_i)\right).\end{displaymath}

Чаще всего в качестве функции $g(y)$ берут $g(y)=y^k$. В этом случае

\begin{displaymath} {\mathsf E}_\theta\, X_1^k = h(\theta),\end{displaymath}

и, если функция $h$ обратима в области $\Theta$, то

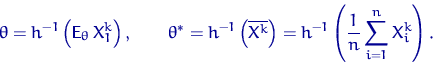
\begin{displaymath} \theta=h^{-1}\left({\mathsf E}_\theta\, X_1^k\right), \qquad... ...X^k}\right)= h^{-1}\left(\dfrac{1}{n}\sum_{i=1}^n X_i^k\right).\end{displaymath}

Можно сказать, что мы берем в качестве оценки такое (случайное) значение параметра $\theta$, при котором истинный момент совпадает с выборочным.

Пример 4.

Пусть $X_1$, $\ldots$, $X_n$ — выборка объема $n$ из равномерного на отрезке $[0,\,\theta]$ распределения ${\mathsf U}_{0,\theta}$, где $\theta\gt$. Найдем оценку метода моментов (ОММ) по первому моменту:

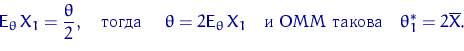
\begin{displaymath} {\mathsf E}_\theta\, X_1 = \dfrac{\theta}{2}, \textrm{\quad ... ..., X_1 \textrm{\quad и ОММ такова\quad} \theta^*_1=2\overline X.\end{displaymath}

Найдем оценку метода моментов (ОММ) по $k$-му моменту:

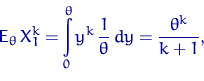
\begin{displaymath} {\mathsf E}_\theta\, X_1^k = \int\limits_0^\theta y^k \,\dfrac{1}{\theta}\,dy = \dfrac{\theta^k}{k+1},\end{displaymath}

тогда

\begin{equation} \theta=\sqrt[k]{(k+1){\mathsf E}_\theta\, X_1^k}, \textrm{\quad и ОММ такова:\quad} \theta^*_k=\sqrt[k]{(k+1)\overline{X^k}}.\end{equation}(4)

Пример 5.

Пусть $X_1$, $\ldots$, $X_n$ — выборка объема $n$ из распределения Пуассона $\text{\boldmath\ensuremath \Pi}_\lambda$ с неизвестным параметром $\lambda\gt$. Введем новый параметр

\begin{displaymath} \theta=\theta(\lambda)={\mathsf P}\,{\!}_\lambda (X_1=1)=\lambda\,e^{-\lambda}\end{displaymath}

и найдем оценку метода моментов для $\theta$ с помощью функции $g(y)={\mathbf I}(y=1)$:

\begin{displaymath} {\mathsf E}\,{\!}_\lambda g(X_1) = {\mathsf E}\,{\!}_\lambda... ...{\mathsf P}\,{\!}_\lambda(X_1=1)=\lambda\,e^{-\lambda}=\theta, \end{displaymath}

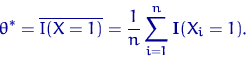
\begin{displaymath} \theta^*=\overline {I(X=1)}=\dfrac{1}{n}\sum\limits_{i=1}^n {\mathbf I}(X_i=1).\end{displaymath}

Заметим, что оценку для параметра $\lambda\gt$ с помощью функции $g(y)={\mathbf I}(y=1)$найти нельзя: функция $h(\lambda)=\lambda\,e^{-\lambda}$ не является взаимно-однозначной и, следовательно, обратимой по $\lambda$ в области $\lambda\gt$. Оценку для параметра $\lambda$ разумно находить по первому моменту: ${\mathsf E}\,{\!}_\lambda X_1 =\lambda$, и $\lambda^*=\overline X$ — оценка метода моментов.

Замечание 6.

Может случиться так, что $\theta^*=h^{-1}(\overline{g(X)})\not\in\Theta$, тогда как $\theta \in \Theta$. В этом случае оценку корректируют. Например, в качестве ОММ берут ближайшую к $h^{-1}(\overline{g(X)})$ точку из $\Theta$ или из замыкания $\Theta$.

Пример 6.

Пусть $X_1$, $\ldots$, $X_n$ — выборка объема $n$ из нормального распределения ${\mathsf N}_{a,1}$ с неотрицательным средним $a\geqslant 0$. Ищем оценку для $a$ по первому моменту:

\begin{displaymath} {\mathsf E}\,{\!}_a X_1 = a, \textrm{\quad поэтому \quad} a^*=\overline X.\end{displaymath}

Однако по условию $a\geqslant 0$, тогда как $\overline X$ может быть и отрицательно. Если $\overline X<0$, то в качестве оценки для $a$ более подойдет 0. Если же $\overline X\gt$, в качестве оценки нужно брать $\overline X$. Итого: $a^*=\max\{0, \overline X\}$ — «исправленная» оценка метода моментов.


N.I.Chernova
9 сентября 2002