Если ![]() — асимптотически нормальная оценка для
— асимптотически нормальная оценка для ![]() , то
, то
![]() состоятельна.
состоятельна.
Доказательство теоремы 6. Вспомним свойство слабой сходимости: произведение двух последовательностей, одна из которых сходится (по вероятности) к постоянной, а другая слабо сходится к некоторой случайной величине, слабо сходится к произведению пределов. Поэтому
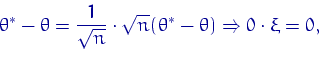
где ![]() имеет нормальное распределение
имеет нормальное распределение ![]() . Но слабая сходимость к нулю влечет сходимость к нулю по вероятности.
. Но слабая сходимость к нулю влечет сходимость к нулю по вероятности.
Q.D.E.
Таким образом, если ![]() асимптотически нормальна, то
асимптотически нормальна, то
![]() , или
, или ![]() . Свойство асимптотической нормальности показывает, в частности,
что скорость этой
сходимости имеет порядок
. Свойство асимптотической нормальности показывает, в частности,
что скорость этой
сходимости имеет порядок ![]() , т.е. расстояние между
, т.е. расстояние между
![]() и
и ![]() ведет себя как
ведет себя как ![]() :
:
![]()
Взглянем с этой точки зрения на оценку в примере
12.
Для нее (и для тех, кто справился с упражнениями)
| (9) |
N.I.Chernova