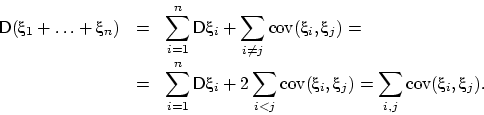Мы знаем, что для
независимых
случайных величин
с конечными
вторыми моментами
дисперсия их суммы равна сумме их дисперсий.
В общем случае, согласно
следствию 16, дисперсия суммы равна
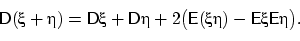 | (19) |
Величина 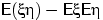 равняется нулю,
если случайные величины
равняется нулю,
если случайные величины  и
и  независимы (свойство (E7) математического ожидания).
С другой стороны, из равенства её нулю вовсе не следует независимость,
как показывают примеры 34 и 35.
Эту величину часто используют как «индикатор наличия зависимости» между
двумя случайными величинами.
независимы (свойство (E7) математического ожидания).
С другой стороны, из равенства её нулю вовсе не следует независимость,
как показывают примеры 34 и 35.
Эту величину часто используют как «индикатор наличия зависимости» между
двумя случайными величинами.
- 2.
- Величина
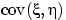 не является «безразмерной»: если
не является «безразмерной»: если  — объем газа
в сосуде, а
— объем газа
в сосуде, а  — давление этого газа, то
ковариация измеряется в м3·Па.
Иначе говоря, при умножении
— давление этого газа, то
ковариация измеряется в м3·Па.
Иначе говоря, при умножении  или
или  на какое-нибудь число ковариация тоже умножается на это число. Но умножение на число
не сказывается на «степени зависимости» величин (они от этого «более
зависимыми» не становятся), так что большое значение ковариации
не означает более сильной зависимости. Это очень плохо.
на какое-нибудь число ковариация тоже умножается на это число. Но умножение на число
не сказывается на «степени зависимости» величин (они от этого «более
зависимыми» не становятся), так что большое значение ковариации
не означает более сильной зависимости. Это очень плохо.
Нужно как-то нормировать ковариацию, получив из неё «безразмерную»
величину, абсолютное значение которой:
а) не менялось бы при умножении случайных величин на число;
б) свидетельствовало бы о «силе зависимости» случайных
величин.
Итак, следующая величина есть всего лишь
ковариация, нормированная нужным образом.
![]() равняется нулю,
если случайные величины
равняется нулю,
если случайные величины ![]() и
и ![]() независимы (свойство (E7) математического ожидания).
С другой стороны, из равенства её нулю вовсе не следует независимость,
как показывают примеры 34 и 35.
Эту величину часто используют как «индикатор наличия зависимости» между
двумя случайными величинами.
независимы (свойство (E7) математического ожидания).
С другой стороны, из равенства её нулю вовсе не следует независимость,
как показывают примеры 34 и 35.
Эту величину часто используют как «индикатор наличия зависимости» между
двумя случайными величинами.