next up previous contents index
Next:  Существование неизмеримых множеств   Up:  Геометрическая вероятность   Previous:  Геометрическая вероятность

§ 1. Определения и примеры

Рассмотрим какую-нибудь область в (на прямой, на плоскости, в пространстве). Предположим, что «мера» (длина, площадь, объем, соответственно) конечна. Пусть случайный эксперимент состоит в том, что мы наудачу бросаем в эту область точку. Термин «наудачу» означает, что вероятность попадания точки в любую часть не зависит от формы или расположения внутри .
Определение 9.

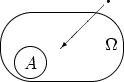
Эксперимент удовлетворяет условиям «геометрического определения вероятности», если его исходы можно изобразить точками некоторой области в так, что вероятность попадания точки в любую часть не зависит от формы или расположения внутри , а зависит лишь от меры области и, следовательно (понять, почему), пропорциональна этой мере:

где обозначает меру области (длину, площадь, объем и т.д.).

Если для точки, брошенной в область , выполнены условия геометрического определения вероятности, то говорят, что точка равномерно распределена в области .
Пример 7. Точка наудачу бросается на отрезок [0, 1]. Вероятность ей попасть в точку 0,5 равна нулю, так как равна нулю мера множества, состоящего из одной точки («длина точки»). Но попадание в точку 0,5 не является невозможным событием — это один из элементарных исходов эксперимента. Общее число элементарных исходов здесь бесконечно, но все они по-прежнему «равновозможны» — уже не в смысле классического определения вероятности, применить которое здесь нельзя из-за бесконечности числа исходов, а в смысле определения 9.

Задача о встрече

Пример 8. Два лица и условились встретиться в определённом месте между двумя и тремя часами дня. Пришедший первым ждет другого в течение 10 минут, после чего уходит. Чему равна вероятность встречи этих лиц, если каждый из них может прийти в любое время в течение указанного часа независимо от другого?

Решение. Будем считать интервал с 14 до 15 часов отрезком [0, 1] длиной в 1 час. Пусть («кси») и («эта») — моменты прихода и — точки отрезка [0, 1]. Все возможные результаты эксперимента  — точки квадрата со стороной 1: 

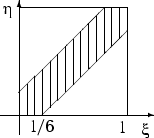
Можно считать, что эксперимент сводится к бросанию точки наудачу в квадрат. При этом благоприятными исходами являются точки множества :

(10 минут = 1/6 часа). Попадание в множество наудачу брошенной в квадрат точки означает, что и встретятся. Тогда вероятность встречи равна

Задача Бюффона(1)

Пример 9. На плоскости начерчены параллельные прямые, находящиеся друг от друга на расстоянии . На плоскость наудачу брошена игла длины . Какова вероятность того, что игла пересечёт какую-нибудь прямую?

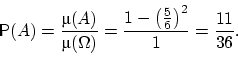
Решение. Поймем, что означает здесь «наудачу брошена игла». 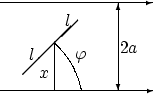Возможные положения иглы (отрезка) на плоскости полностью определяются положением середины иглы и углом поворота иглы относительно какого-либо направления. Причём две эти переменные (положение центра и угол поворота) меняются независимо друг от друга. Обозначим через расстояние от середины иглы до ближайшей прямой, а через — угол между каким-то направлением прямых и иглой. 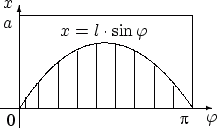Множество возможных положений иглы целиком определяется выбором наудачу точки из прямоугольника .

Игла пересекает ближайшую прямую, если координаты выбранной наудачу точки удовлетворяют неравенству: . Площадь области , точки которой удовлетворяют такому неравенству, равна

Поделим на и получим, что искомая вероятность равна .


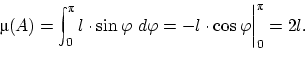
1Georges Louis Leclerc Comte de Buffon (7.09.1707 — 16.04.1788, France) .

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

N.Ch.