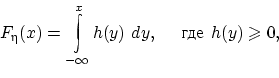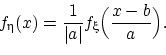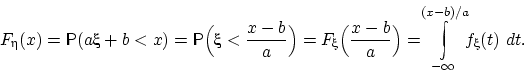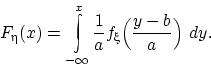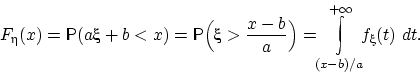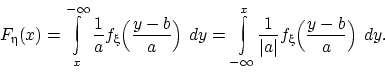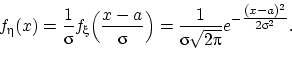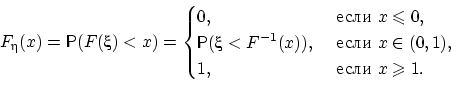



Next: Многомерные распределения
Up: Преобразования случайных величин
Previous: Измеримость функций от случайных
Если случайная величина

имеет
дискретное распределение, то для любой
борелевской функции 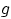
величина
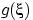
также имеет дискретное распределение,
и таблица распределения
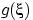
находится просто по определению.
Поэтому мы будем рассматривать в основном преобразования случайных величин
с
абсолютно непрерывными распределениями.
Пусть случайная величина  имеет функцию распределения
имеет функцию распределения 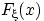 и плотность
распределения
и плотность
распределения 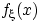 . Построим с помощью борелевской
функции
. Построим с помощью борелевской
функции 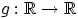 случайную величину
случайную величину 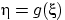 .
Требуется найти функцию распределения и, если существует, плотность
распределения величины
.
Требуется найти функцию распределения и, если существует, плотность
распределения величины 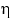 .
.
Упражнение 34.
Привести пример плотности распределения случайной величины

и
непрерывной функции
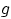
таких, что
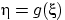
имеет:
а) дискретное распределение;
б) невырожденное дискретное распределение.
Плотность распределения величины
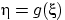
заведомо существует, если,
например, функция
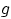
(строго) монотонна.
В общем случае мы не можем просто продифференцировать функцию распределения,
поскольку не знаем, существует ли плотность.
Следует доказать, что распределение абсолютно непрерывно.
Но доказывая это, мы попутно найдём и плотность распределения.
Действительно, у нас есть следующий путь доказательства
абсолютной непрерывности распределения.
Если, согласно равенству (14),
можно для любого 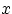 представить функцию распределения величины
представить функцию распределения величины 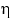 в виде
в виде
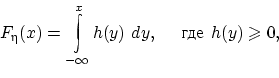
то плотность распределения величины 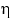 существует и
равна подынтегральной функции:
существует и
равна подынтегральной функции: 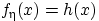 .
Другой путь — продифференцировать функцию распределения и уже затем убедиться, что производная
является плотностью распределения, т.е. обладает свойствами (f1) и (f2).
.
Другой путь — продифференцировать функцию распределения и уже затем убедиться, что производная
является плотностью распределения, т.е. обладает свойствами (f1) и (f2).
Теорема 23.
Пусть

имеет функцию распределения
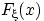
и плотность
распределения
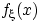
, и постоянная
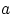
отлична от нуля.
Тогда случайная величина
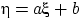
имеет плотность распределения
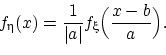
Для произвольной монотонной функции
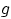
справедливо утверждение:
Теорема 24.
Пусть

имеет плотность
распределения
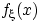
, и функция
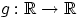
монотонна.
Тогда случайная величина
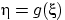
имеет плотность распределения
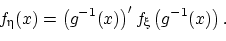
Здесь 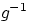 — функция, обратная к
— функция, обратная к 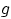 , и
, и 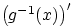 — её производная.
— её производная.
Упражнение 35.
Доказать теорему
24.
Из теоремы
23 следуют уже знакомые нам утверждения:
Следствие 4.
Если
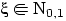
, то
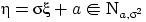
.
Доказательство.
Действительно,
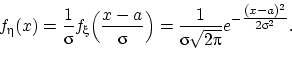
QED
Следствие 5.
Если
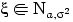
, то
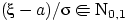
.
Следствие 6.
Если
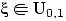
, то
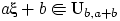
при
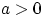
.
Следствие 7.
Если

, то
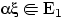
.
Теорема 25.
Пусть функция распределения
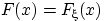
непрерывна. Тогда случайная
величина
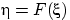
имеет
равномерное на отрезке [0, 1] распределение.
Теорему
25 можно использовать для построения случайных величин
с заданным распределением по равномерно распределённой случайной величине
(например, по результату ДСЧ). Следующее утверждение верно не только
для непрерывных, но для любых функций распределения
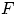
.
Обозначим через
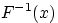
точную нижнюю грань множества тех
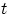
, для которых
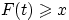
:
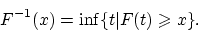
Для непрерывной функции  это определение «обратной функции» совпадает с введённым в доказательстве
теоремы 25.
это определение «обратной функции» совпадает с введённым в доказательстве
теоремы 25.
Теорема 26.
Пусть
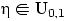
, а
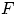
— произвольная
функция распределения. Тогда случайная
величина
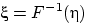
(
«квантильное преобразование» над случайной величиной
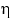
) имеет функцию распределения
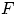
.
Следствие 8.
Пусть
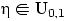
. Верны соотношения:
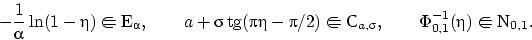




Next: Многомерные распределения
Up: Преобразования случайных величин
Previous: Измеримость функций от случайных
N.Ch.
![]() имеет функцию распределения
имеет функцию распределения ![]() и плотность
распределения
и плотность
распределения ![]() . Построим с помощью борелевской
функции
. Построим с помощью борелевской
функции ![]() случайную величину
случайную величину ![]() .
Требуется найти функцию распределения и, если существует, плотность
распределения величины
.
Требуется найти функцию распределения и, если существует, плотность
распределения величины ![]() .
.