Вопрос об
измеримости 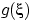
решает следующая теорема.
Доказательство.
Проверим, что прообраз любого борелевского множества
при отображении
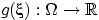
является
событием.
Возьмём произвольное
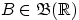
и положим
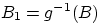
.
Множество
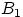
борелевское, так как функция
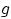
измерима по Борелю. Найдём
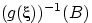
:
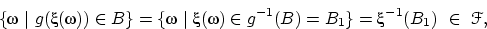
поскольку  и
и  — случайная величина.
— случайная величина.
QED
Борелевскими являются все привычные нам функции.
Функцией, неизмеримой по Борелю, будет, например,
индикаторная
функция неизмеримого множества Витали, т.е. функция, принимающая значение 1 в точках этого множества и значение 0 во всех прочих точках числовой прямой.
Вообще говоря,
неизмеримые функции суть объекты экзотические, в обычной жизни
не встречающиеся.
![]()
![]() и
и ![]() — случайная величина.
— случайная величина.