Примеры

Найдем ОМНК для функций

в ряде частных случаев. Напомним, что ОМП совпадает с ОМНК почти исключительно в случае нормальности вектора ошибок.

Пример 35.

Пусть функция $f(t)=\theta$ — постоянная, $\theta$ — неизвестный параметр. Тогда наблюдения равны $X_i=\theta+\varepsilon_i$ , $i=1, \ldots, n$ . Легко узнать задачу оценивания неизвестного математического ожидания $\theta$ по выборке из независимых и одинаково распределенных случайных величин $X_1, \ldots, X_n$ . Найдем ОМНК $\hat\theta$ для параметра $\theta$ :

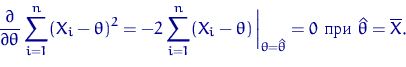
$\begin{displaymath} \dfrac{\partial}{\partial\theta} \sum_{i=1}^n(X_i-\theta)^2=... ...{\theta=\hat\theta} = 0 \textrm{ при } \hat\theta=\overline X.\end{displaymath}$

Трудно назвать этот ответ неожиданным. Соответственно, $\hat{\sigma^{2}} = S^2$ .

Упражнение. Покажите, что в условиях примера 34 ОМП для $\theta$ , минимизирующая $\sum \lvert X_i-\theta \rvert$ , есть выборочная медиана

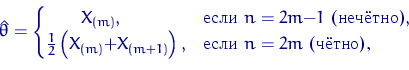
$\begin{displaymath} \hat\theta=\begin{cases} \qquad X_{(m)}, & \textrm{если } n=... ...1)}\right), & \textrm{если } n=2m \textrm{ (чётно),}\end{cases}\end{displaymath}$

а ОМП для дисперсии равна $\hat\sigma^2=\tfrac{1}{n}\sum\limits_{i=1}^n\lvert X_i-\hat \theta\rvert$ . Вместо полусуммы можно брать любую точку отрезка $\left[X_{(m)},\,X_{(m+1)}\right]$ .

Пример 36. Линейная регрессия.

Рассмотрим линейную регрессию $X_i=\theta_1+t_i\theta_2+\varepsilon_i$ , $i=1, \ldots, n$ , где $\theta_1$ и $\theta_2$ — неизвестные параметры. Здесь $f(t)=\theta_1+t\theta_2$ — прямая.

Найдем оценку метода наименьших квадратов $\hat\theta_1,\hat\theta_2$ , на которой достигается минимум величины $\sum\varepsilon_i^2=\sum(X_i-\theta_1-t_i\theta_2)^2$ . Приравняв к нулю частные производные этой суммы по параметрам, найдем точку экстремума.

Упражнение. Убедиться, что решением системы уравнений

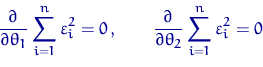
$\begin{displaymath} \dfrac{\partial}{\partial\theta_1} \sum_{i=1}^n \varepsilon_... ...ac{\partial}{\partial\theta_2} \sum_{i=1}^n \varepsilon_i^2 = 0\end{displaymath}$

является пара

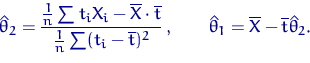
$\begin{displaymath} \hat\theta_2= \dfrac{\tfrac{1}{n}\sum t_iX_i-\overline X\cdo... ..., \quad \quad \hat\theta_1=\overline X-\overline t\hat\theta_2.\end{displaymath}$

Определение 32.

Величина

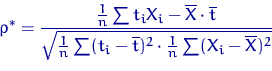
$\begin{displaymath} \rho^*=\dfrac{\tfrac{1}{n}\sum t_iX_i-\overline X\cdot\overl... ...um(t_i-\overline t)^2\cdot\tfrac{1}{n}\sum(X_i-\overline X)^2}}\end{displaymath}$

называется выборочным коэффициентом корреляции и характеризует степень линейной зависимости между наборами чисел $X_1, \ldots, X_n$ и $t_1,\ldots,t_n$ .

Пример 37.

Термин «регрессия» появился впервые в работе Francis Galton, "Regression towards mediocrity in hereditary stature" (Journal of the Anthropological Institute V. 15, p. 246-265, 1886).

Гальтон исследовал, в частности, рост детей высоких родителей и установил, что он «регрессирует» в среднем, т.е. в среднем дети высоких родителей не так высоки, как их родители. Пусть — рост сына (дочери), а и — рост отца и матери. Для линейной модели регрессии ${\mathsf E}\,(X~\lvert~Z_1=t,Z_2=u)=f(t,u)= \theta_1t+\theta_2u+c$ Гальтон нашел оценки параметров:

$\begin{displaymath} {\mathsf E}\,(\textrm{роста сына}~\lvert~Z_1=t,Z_2=u) = 0,27 t + 0,2 u + \mathop{const},\end{displaymath}$

а средний рост дочери еще в 1,08 раз меньше.

9.4. Примеры