Асимптотически нормальные оценки (АНО)

Для того, чтобы уметь сравнивать оценки вида $\theta^*_k=\sqrt[k]{(k+1)\overline{X^k}}$ (см. пример 4), среднеквадратического подхода недостаточно: второй момент такой случайной величины посчитать вряд ли удастся. Оценки такого вида (функции от сумм) удается сравнивать с помощью асимптотического подхода. Более точно, этот подход применим к так называемым «асимптотически нормальным» оценкам.

Пусть

, $\ldots$ ,

— выборка объема

из параметрического семейства распределений $\mathscr F_\theta$ , $\theta \in \Theta$ .

Пример 12.

Пусть , $\ldots$ , — выборка объема из равномерного распределения ${\mathsf U}_{0,\theta}$ , где $\theta\gt$ . Проверим, являются ли оценки $\theta^*=2\overline X$ и $\hat\theta=X_{(n)}$ асимптотически нормальными (АНО). По ЦПТ,

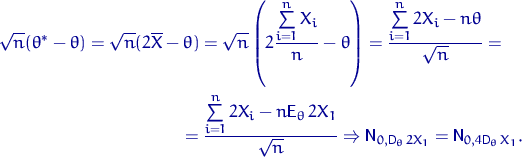
$\begin{multline*} \sqrt{n}(\theta^*-\theta) = \sqrt{n}(2\overline X-\theta) = \s... ...sf D}_\theta\, 2X_1} = {\mathsf N}_{0,4{\mathsf D}_\theta\, X_1}.\end{multline*}$

То есть оценка $\theta^*=2\overline X$ асимптотически нормальна с коэффициентом

$\begin{displaymath} \sigma^2(\theta)=4{\mathsf D}_\theta\, X_1=4\theta^2/12=\theta^2/3.\end{displaymath}$

Для оценки $\hat\theta=X_{(n)}$ имеем:

$\begin{equation} \sqrt{n}(\hat\theta-\theta)=\sqrt{n}(X_{(n)}-\theta) < 0 \textrm{ с вероятностью } 1.\end{equation}$ (8)

По определению, $\xi_n\Rightarrow F$ , если для любой точки , являющейся точкой непрерывности функции распределения , имеет место сходимость $F_{\xi_n}(x)={\mathsf P}\,(\xi_n<x)\to F(x)$ .

Но ${\mathsf P}_\theta\,(\sqrt{n}(X_{(n)}-\theta) < 0)=1$ , тогда как для нормального распределения ${\mathsf N}_{0,\sigma^2(\theta)}$ функция распределения всюду непрерывна, и в нуле равна $\Phi_{0,\sigma^2(\theta)}(0)=0.5$ . Но 1 не сходится к 0.5 при $n\to\infty$ , поэтому слабая сходимость $\sqrt{n}(X_{(n)}-\theta)$ к ${\mathsf N}_{0,\sigma^2(\theta)}$ места не имеет.

Таким образом, оценка асимптотически нормальной не является. Осталось ответить на напрашивающиеся вопросы:

1)

Куда все же сходится по распределению $\sqrt{n}(X_{(n)}-\theta)$ ?

Упражнение. Доказать, что $\sqrt{n}(X_{(n)}-\theta)\Rightarrow 0$ .

Порядок действий: Выписать определение слабой сходимости. Нарисовать функцию распределения нуля. Найти по определению функцию распределения $\sqrt{n}(X_{(n)}-\theta)$ . Убедиться, что она сходится к функции распределения нуля во всех точках непрерывности последней. Не забудьте о существовании замечательных пределов, логарифмов и ряда Тейлора.

2)

Если $\sqrt{n}(X_{(n)}-\theta)\Rightarrow 0$ , то на какую степень

нужно попробовать умножить $X_{(n)}-\theta$ , чтобы получить сходимость к величине, отличной от 0 и $\infty$ ?

Упражнение. Доказать, что $-n(X_{(n)}-\theta)\Rightarrow \eta$ , где случайная величина $\eta$ имеет показательное распределение ${\mathsf E}\,{\!}_{1/\theta}$ .

Порядок действий: прежний.

3)

Для оценки $\dfrac{n+1}{n} X_{(n)}$ свойство (8) не выполнено. Может ли эта оценка быть АНО?

Упражнение. Модифицировать рассуждения и доказать, что эта оценка тоже не является асимптотически нормальной.

4)

Плохо ли, что оценка не асимптотически нормальна? Может быть, сходимость $n (X_{(n)}-\theta)\Rightarrow -\eta$ еще лучше?

3.3. Асимптотически нормальные оценки (АНО)