Классическое вероятностное пространство

Next: Геометрические вероятности Up: Оглавление Previous: Операции над событиями

2. Классическое вероятностное пространство

2.1. а) 1/2; б) 3/8; в) 7/8.

2.2. $AB=\{\textrm{\itshape на одной из костей выпала единица, на другой --- четное число очков}\}$ , $\mathsf P\{AB\}=\displaystyle\frac16$ , $\mathsf P\{A\cup B\}=\displaystyle\frac{23}{36}$ , $\mathsf P\{\overline{AB}\}=\displaystyle\frac56$ , $\mathsf P\{A\overline B\}=\displaystyle\frac13$ .

2.3. $\displaystyle\frac{3!\cdot 2!\cdot 2!}{10!}$ = $6{,}6(137566)\cdot 10^{-6}$ .

2.4. а) $\displaystyle\frac{1}{8^5}$ = $3{,}0517578125\cdot 10^{-5}$ ; б) $\displaystyle\frac{1}{8^4}$ = $2{,}44140625\cdot 10^{-4}$ ; в) $\displaystyle\frac{A_8^5}{8^5}$ = .

2.5. 0,096.

2.6. а) $\displaystyle\frac{A_{10}^4}{10^4}$ = ; б) $\displaystyle\frac{C_{10}^2C_4^2}{10^4}$ = ; в) $\displaystyle\frac{A_{10}^3C_4^2}{10^4}$ = ; г) $\displaystyle\frac{4A_{10}^2}{10^4}$ = ; д) ; е) .
Указание: в ответах считается, что номер 0000 возможен.

2.7. $\displaystyle\frac{1}{6^3}$ .

2.8. $\displaystyle\frac{C_{10}^2+C_6^2}{C_{16}^2}$ = .

2.9. $1-\displaystyle\frac{10\cdot C_{27}^3-C_{10}^2}{C_{30}^6}$ = $\displaystyle\frac{12\,546}{13\,195}$ .

2.10. 28/29.

2.11. Например, $\Omega$ -- множество неупорядоченных наборов по 6 карт; а) 6/52; б) $\displaystyle\frac{C_4^2\cdot{13}^2\cdot\left(C_{\!13}^2\right)^2+4\cdot{13}^3\cdot C_{\!13}^3}{C_{52}^6}$ = 83486/195755; наименьшее число карт — 6.

2.14. а) $\displaystyle\frac{4\cdot C_{32}^2}{C_{36}^3}$ = 496/1785; б) $1-\displaystyle\frac{C_{32}^3}{C_{36}^3}$ = 109/357; в) на березах яблоки не растут.

2.15. а) $\displaystyle\frac{C_4^2\,C_{32}^{16}}{C_{36}^{18}}$ = 153/385; б) $2\cdot\displaystyle\frac{C_{32}^{18}}{C_{36}^{18}}$ = 8/77; в) $\displaystyle\frac{{\left(C_{\!18}^9\right)}^2}{C_{36}^{18}}$ = 2149004/8250123.

2.16. а) $\displaystyle\frac{1}{(N{-}1)}$ ; б) $\displaystyle\frac{1}{(N{-}1)(N{-}2)}$

2.17. $2\cdot\displaystyle\frac{N{-}r{-}1}{N(N{-}1)}$ .

2.18. а) $\displaystyle\frac{1}{n}$ ; б) $\displaystyle\frac{1}{n(n{-}1)}$ .

2.19. $\displaystyle\frac{2}{n}$ .

2.20. $\sum\limits_{k=m}^n \displaystyle\frac{M{-}1}{N}\cdot\frac{M{-}2}{N{-}1} \cdot\ldots\cdot\frac{M{-}k}{N{-}k{+}1}$ ; предел равен $\sum\limits_{k=m}^n \alpha^k$ .

2.21. $1-\displaystyle\frac{C_{n-m}^k}{C_n^k}$ .

2.22. 2/5.

2.23. а), б) $\displaystyle\frac{9^r}{10^r}$ ; в) $\displaystyle\frac{8^r}{10^r}$ ; г) $\displaystyle\frac{A_{10}^r}{10^r}$ при $r\leqslant 10$ ; д) $\displaystyle\frac{2\cdot 9^r-8^r}{10^r}$ .

2.24. а), б) 3/5; в) 3/10.

2.25. $1-\left(\displaystyle\frac{35}{36}\right)^n$ .

2.26. $\displaystyle\frac{C_M^mC_{N-M}^{n-m}}{C_N^n}$ ; $\sum\limits_{k=0}^m\displaystyle\frac{C_M^kC_{N-M}^{n-k}}{C_N^n}$

2.27. $1-\displaystyle\frac{1}{2!}+\displaystyle\frac{1}{3!}-\ldots+(-1)^{n-1} \displaystyle\frac{1}{n!}$ .

2.28. а) См. 2.27; б) $\displaystyle\frac{1}{m!}$ .

2.29. См. 2.27; $\lim\limits_{n\to\infty}p_n=1-e^{-1}$ .

2.30. $\displaystyle\frac{1}{C_{49}^6}$ = $\displaystyle\frac{1}{13983816}\approx 7{,}15\cdot 10^{-8}$ ; $\displaystyle\frac{6\cdot43}{C_{49}^6}$ = $\displaystyle\frac{43}{2330636}\approx 1{,}845\cdot 10^{-5}$ ; $\displaystyle\frac{C_6^4\cdot C_{43}^2}{C_{49}^6}$ = $\displaystyle\frac{645}{665896}\approx 0{,}00097$ ; $\displaystyle\frac{C_6^3\cdot C_{43}^3}{C_{49}^6}$ = $\displaystyle\frac{8815}{499422}\approx 0{,}01765$ ; $\displaystyle\frac{C_6^2\cdot C_{43}^4}{C_{49}^6}$ = $\displaystyle\frac{132225}{998844}\approx 0{,}132$ ; $\displaystyle\frac{6\cdot C_{43}^5}{C_{49}^6}$ = $\displaystyle\frac{68757}{166474}\approx 0{,}413$ ; $\displaystyle\frac{C_{43}^6}{C_{49}^6}$ = $\displaystyle\frac{435461}{998844}\approx 0{,}436$ .

2.31. $\displaystyle\frac{C_{80}^{10}}{C_{90}^{10}}$ $\approx 0,2878$ .

2.32. а) $\displaystyle\frac{1}{6^3}$ ; б) $\displaystyle\frac{A_6^3\cdot 3!+3\cdot A_6^2\cdot 3+6}{6^6}$ = $\displaystyle\frac{166}{6^5}$ .

2.33. $\displaystyle\frac{1}{n{+}1}$ .

2.34. а) $\displaystyle\frac{n!}{n^n}$ ; б) $\displaystyle\frac{n!\cdot C_n^2}{n^n}$ .

2.35. $\displaystyle\frac{1}{C_{n+r-1}^r}$ ; $\displaystyle\frac{C_{n+r-2-k}^{r-k}}{C_{n+r-1}^r}$ .

2.36. .

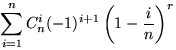2.37. а) $\displaystyle\frac{C_r^s\cdot (n-1)^{r-s}}{n^r}$ ; б) $\displaystyle\sum\limits_{i=1}^nC_n^i(-1)^{i+1}\left(1-\frac{i}{n}\right)^r$ .
Указание: используя формулу включения-исключения, вычислить вероятность объединения событий $A_i=\{\textrm{ящик с номером}$ $\textrm{пуст}\}$ , $i=1,\ldots,n$ .

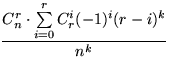2.38. а) $\displaystyle\frac{C_n^r\cdot\sum\limits_{i=0}^rC_r^i(-1)^i(r-i)^k}{n^k}$ .
Указание: воспользоваться решением задачи 2.37(б);
б) $\displaystyle\frac{k!}{k_1!\cdot\ldots\cdot k_n!}\cdot\displaystyle\frac{1}{n^k}$ ; в) при $k_i=0\vee 1$ для всех , $k_1+\ldots+k_n=k$ ; если же $\displaystyle\frac{k}{n}=l$ -- целое, то при $k_1=\ldots=k_n=l$ .

2.39. а) $\displaystyle\frac{n!\cdot 2^n}{(2n)!}$ ; б) $\displaystyle\frac{(n!)^2\cdot 2^n}{(2n)!}$ .

2.40. а) $\displaystyle{\left(1-\frac1n\right)}^{r-1}$ ; б) $\displaystyle\frac{A_n^r}{n^r}$ .

2.41. а) $\displaystyle{\left(1-\frac{N}{n}\right)}^{r-1}$ ; б) $\displaystyle\frac{C_{n-N}^N\cdot C_{n-2N}^N\cdot\ldots\cdot C_{n-(r-1)N}^N}{\left(C_n^N\right)^{r-1}}$ .

2.42. а) $\displaystyle\frac{12!}{12^{12}}$ = $\displaystyle\frac{1925}{35831808}\approx 5{,}37\cdot 10^{-5}$ ; б) $\displaystyle\frac{C_{12}^2\cdot(2^6-2)}{12^6}$ = $\displaystyle\frac{341}{12^5}\approx 0{,}00137$ .

2.43. $\displaystyle\frac{30!}{{\left(2!\right)}^6\cdot{\left(3!\right)}^6}\cdot\displaystyle\frac{12!}{{12}^{30}}$ .

2.44. $1-\displaystyle\frac{A_{365}^n}{365^n}$ .

2.45. а) $\displaystyle\frac{C_n^r\cdot 2^r}{C_{2n}^r}$ ; б) $\displaystyle\frac{n\cdot C_{n-1}^{r-2}\cdot 2^{r-2}}{C_{2n}^r}$ ; в) $\displaystyle\frac{C_n^2\cdot C_{n-2}^{r-4}\cdot 2^{r-4}}{C_{2n}^r}$ ; г) $1-\displaystyle\frac{C_n^r\cdot 2^r}{C_{2n}^r}$ .