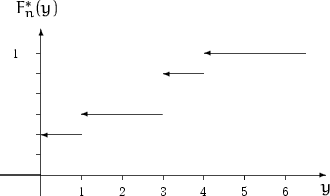
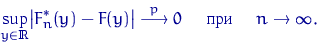
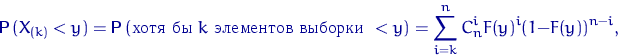
где ![]() — функция распределения величины
— функция распределения величины ![]() .
.
![\begin{displaymath}
{\left(\overline{X^k}\right)}^{\frac{1}{k}}=
\sqrt[k]{ \left(\frac{1}{n}\sum_{i=1}^n X_i^k\right) }\end{displaymath}](img175.gif)
а) стремится к ![]() при
при ![]() ;
;
б) стремится к ![]() при
при ![]() .
.
Имеется в виду сходимость для любого набора чисел ![]() , такого, что среднее степенное определено, т.е. сходимость п.н.
, такого, что среднее степенное определено, т.е. сходимость п.н.
Указание. Вынести ![]() (или
(или ![]() ) из-под корня,
воспользоваться леммой о двух милиционерах и свойствами:
) из-под корня,
воспользоваться леммой о двух милиционерах и свойствами:
![]() при
при ![]() ,
,
![]() при
при ![]() , и т.д.
, и т.д.
![\begin{displaymath}
\sqrt[k]{{\mathsf E}\,(\xi^*)^k}=\sqrt[k]{\left(\frac{1}{n}\sum_{i=1}^n X_i^k\right)}, \quad k=1,2,3,\ldots\end{displaymath}](img182.gif)
не убывает по ![]() .
.
Указание. Воспользоваться неравенством Йенсена.