Проверка гипотезы однородности

Даны две выборки ${\mathbf X}=(X_1, \ldots, X_n)$ и ${\mathbf Y}=(Y_1,\ldots,Y_m)$ из неизвестных распределений $\mathscr F$ и $\mathscr G$ соответственно. Проверяется сложная гипотеза $H_1=\{\mathscr F= \mathscr G\}$ против (еще более сложной) альтернативы $H_2=\{H_1\textrm{ неверна}\}$ .

Критерий Колмогорова — Смирнова используют, если $\mathscr F$ и $\mathscr G$ имеют непрерывные функции распределения.

Пусть

— эмпирические функции распределения, построенные по выборкам ${\mathbf X}$ и ${\mathbf Y}$ ,

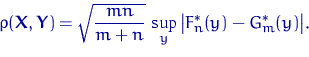
$\begin{displaymath} \rho({\mathbf X},{\mathbf Y})=\sqrt{\frac{mn}{m+n}}\, \sup_y\, \bigl\lvert F_n^*(y)-G_m^*(y)\bigr\rvert.\end{displaymath}$

Теорема 9.

Если гипотеза верна, то $\rho({\mathbf X},{\mathbf Y}) \Rightarrow \eta$ при $n,m\to\infty$ , где $\eta$ имеет распределение с функцией распределения Колмогорова.

И снова: в таблице распределения Колмогорова по заданному $\varepsilon$ найдем

такое, что $\varepsilon={\mathsf P}\,(\eta\geqslant C)$ , и построим критерий согласия Колмогорова — Смирнова:

$\begin{displaymath} \delta({\mathbf X})=\begin{cases} H_1, & \textrm{если }\rho... ..._2, & \textrm{если }\rho({\mathbf X})\geqslant C. \end{cases} \end{displaymath}$

Замечание 23.

Если есть более двух выборок, и требуется проверить гипотезу однородности, часто пользуются одним из вариантов критерия $\chi^2$ Пирсона. Этот критерий (и ряд других критериев) рекомендую посмотреть в §3.4.2, с. 124 книги Г.И.Ивченко, Ю.И.Медведев. Математическая статистика. Москва, 1984, 248 с.

8.4. Проверка гипотезы однородности