next up previous index
Next:  Проверка гипотезы однородности   Up:  Критерии согласия   Previous:  Критерии согласия: критерий Пирсона

8.3.   Критерий $\chi^2$ Пирсона для проверки параметрической гипотезы

Критерий $\chi^2$ часто применяют для проверки гипотезы о виде распределения, т.е. о принадлежности распределения выборки некоторому параметрическому семейству. Имеется выборка ${\mathbf X}=(X_1, \ldots, X_n)$ из неизвестного распределения $\mathscr F$. Проверяется сложная гипотеза

\begin{displaymath} H_1=\bigl\{\mathscr F \in\{\mathscr F_\theta\}\bigr\},\end{displaymath}

где $\theta\in\Theta\subseteq{\textrm{\upshape I\kern-0.20em R}}^l$ — неизвестный параметр (скалярный или векторный), $l$ — его размерность.

Пусть ${\textrm{\upshape I\kern-0.20em R}}$ разбито на $k\gt l$ интервалов группировки $A_1\cup\ldots\cup A_k$, и $\nu_j$ -- число элементов выборки, попавших в $A_j$. Но вероятность $p_j = {\mathsf P}\,{\!}_{H_1}(X_1\in A_j)=p_j(\theta)$ теперь зависит от неизвестного параметра $\theta$.

Функция отклонения (23) также зависит от неизвестного параметра $\theta$, и использовать ее в критерии Пирсона нельзя — мы не можем вычислить ее значение:

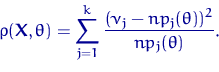\begin{equation} \rho({\mathbf X},\theta)= \sum_{j=1}^k \dfrac{(\nu_j-n p_j(\theta))^2}{n p_j(\theta)}.\end{equation}(24)

Пусть $\hat\theta=\hat\theta({\mathbf X})$ — значение параметра $\theta$, доставляющее минимум функции $\rho({\mathbf X},\theta)$ при данной выборке ${\mathbf X}$. Подставив вместо истинных вероятностей $p_j$ их оценки $p_j(\hat\theta)$, получим функцию отклонения

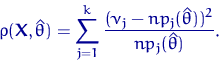\begin{equation} \rho({\mathbf X},\hat\theta)= \sum_{j=1}^k \dfrac{(\nu_j-n p_j(\hat\theta))^2}{n p_j(\hat\theta)}.\end{equation}(25)

Условие K1(a) (при выполнении некоторых условий относительно гладкости $p_j(\theta)$)(*)  обеспечивается теоремой (R. Fisher, 1924), которую мы доказывать не будем:


Теорема 8.

Если верна гипотеза $H_1$, и $\mathop{dim}(\theta)=l$ — размерность параметра (вектора) $\theta$, то при фиксированном $k$ и при $n\to\infty$

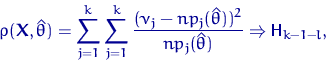
\begin{displaymath} \rho({\mathbf X},\hat\theta)= \sum_{j=1}^k \sum_{j=1}^k \df... ...\theta))^2}{n p_j(\hat\theta)} \Rightarrow {\mathsf H}_{k-1-l},\end{displaymath}

где ${\mathsf H}_{k-1-l}$ есть $\chi^2$-распределение с $k-1-l$ степенями свободы.


Условие K1(б) выполнено, если, скажем, рассматривать альтернативные распределения $\mathscr F_2$ такие, что ни при каких $\theta$ набор вероятностей ${\mathsf P}\,{\!}_{\mathscr F_2}\!(X_1{\in}A_1),\ldots,{\mathsf P}\,{\!}_{\mathscr F_2}\!(X_1{\in}A_k)$ не совпадает с $p_1(\theta),\ldots,p_k(\theta)$.

Построим критерий $\chi^2$.

Пусть случайная величина $\chi^2_{k-1-l}$ имеет распределение ${\mathsf H}_{k-1-l}$. По заданному $\varepsilon$ найдем $C$ такое, что $\varepsilon={\mathsf P}\,(\chi^2_{k-1-l}\geqslant C)$.

Критерий согласия $\chi^2$ имеет такой же вид, как все критерии согласия:

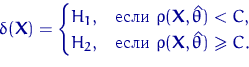
\begin{displaymath} \delta({\mathbf X})=\begin{cases} H_1, & \textrm{если }\rho... ...trm{если }\rho({\mathbf X},\hat\theta)\geqslant C. \end{cases}\end{displaymath}

Замечания 19, 20 о количестве интервалов разбиения остаются в силе.

Замечание 21.

Оценку $\hat\theta$, минимизирующую функцию $\rho({\mathbf X},\theta)$, нельзя заменить на оценку максимального правдоподобия для $\theta$, построенную по выборке $X_1$,  $\ldots$,  $X_n$. При такой замене предельное распределение величины $\rho({\mathbf X},\theta)$

а) уже не равно ${\mathsf H}_{k-1-l}$, а совпадает с распределением величины

\begin{displaymath} \xi_1^2+\ldots+\xi_{k-1-l}^2\textcolor{blue}{+a_1(\theta)\xi_{k-l}^2+\ldots+a_l(\theta)\xi_{k-1}^2},\end{displaymath}

где все $\xi_i$ независимы и имеют распределение ${\mathsf N}_{0,1}$, а коэффициенты $a_i(\theta)$, вообще говоря, отличны от 0 и 1 (H.Chernoff, E.Lehmann, 1954);

б) зависит от $\theta$.

Почувствуйте разницу:

Замечание 22.

Оценку $\hat\theta$, минимизирующую функцию $\rho({\mathbf X},\theta)$, можно получить как оценку максимального правдоподобия для $\theta$, построенную по вектору $\nu_1$, $\ldots$, $\nu_k$ из полиномиального распределения. Функция правдоподобия имеет вид

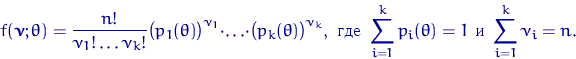
\begin{displaymath} f(\text{\boldmath\ensuremath \nu}; \theta)=\frac{n!}{\nu_1!\... ...де } \sum_{i=1}^kp_i(\theta)=1 \textrm{ и }\sum_{i=1}^k\nu_i=n.\end{displaymath}

Вычисление точки максимума по $\theta$ такой функции в общем случае возможно лишь численно, равно как и вычисление точки минимума функции $\rho({\mathbf X},\theta)$.


N.I.Chernova
9 сентября 2002

(*) Все $\partial^2 p_j(\theta)/\partial\theta_i\partial\theta_l$ непрерывны по $\theta$; ранг матрицы $\lVert\partial p_j(\theta)/\partial\theta_i\rVert$ равен $l$.