Имеется выборка ![]() из распределения
из распределения ![]() . Проверяется простая гипотеза
. Проверяется простая гипотеза ![]() против сложной альтернативы
против сложной альтернативы ![]() . В том случае, когда распределение
. В том случае, когда распределение ![]() имеет непрерывную
функцию распределения
имеет непрерывную
функцию распределения ![]() , можно пользоваться критерием Колмогорова.
Пусть
, можно пользоваться критерием Колмогорова.
Пусть
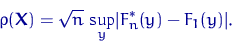
Покажем, что ![]() удовлетворяет условиям K1(a,б).
удовлетворяет условиям K1(a,б).
![]()
Умножая на ![]() , получим при
, получим при ![]() , что
, что
![]()
|
Пусть случайная величина
Это распределение табулировано, так что по заданному |
Критерий Колмогорова выглядит так:

N.I.Chernova