Пусть, как обычно, имеется выборка ![]() из распределения
из распределения ![]() с неизвестным параметром
с неизвестным параметром
![]() . До сих пор мы занимались
«точечным оцениванием» неизвестного параметра — находили
число («оценку»), способную, в некотором смысле,
заменить параметр.
. До сих пор мы занимались
«точечным оцениванием» неизвестного параметра — находили
число («оценку»), способную, в некотором смысле,
заменить параметр.
Существует другой подход к оцениванию, при котором мы указываем
интервал, накрывающий параметр с заданной наперед вероятностью.
Такой подход называется «интервальным оцениванием». Сразу заметим:
чем больше уверенность в
том, что параметр лежит в интервале, тем шире интервал. Так что
мечтать найти диапазон, в котором ![]() лежит с вероятностью 1,
бессмысленно — это вся область
лежит с вероятностью 1,
бессмысленно — это вся область ![]() .
.
Пусть ![]() . Интервал
. Интервал
![]() называется доверительным интервалом для параметра
называется доверительным интервалом для параметра ![]() уровня доверия
уровня доверия ![]() , если для любого
, если для любого ![]()
![]()
Пусть ![]() . Интервал
. Интервал
![]() называется асимптотическим доверительным интервалом
для параметра
называется асимптотическим доверительным интервалом
для параметра ![]() (асимптотического)
уровня доверия
(асимптотического)
уровня доверия ![]() , если для любого
, если для любого ![]()
![]()
На самом деле в определении 14 речь идет, конечно, не об одном
интервале, но о последовательности интервалов,
зависящих от объема выборки ![]() .
.
Случайны здесь границы интервала ![]() , поэтому читают
формулу
, поэтому читают
формулу ![]() как «интервал
как «интервал
![]() накрывает параметр
накрывает параметр ![]() », а не как
«
», а не как
«![]() лежит в интервале...».
лежит в интервале...».
Неравенство «![]()
![]() » обычно соответствует дискретным
распределениям, когда нельзя обязаться добиться равенства:
например, для
» обычно соответствует дискретным
распределениям, когда нельзя обязаться добиться равенства:
например, для ![]() при любом
при любом ![]() равенство
равенство
![]() невозможно, а неравенство имеет смысл:
невозможно, а неравенство имеет смысл:
![]()
Если вероятность доверительному интервалу накрывать параметр в точности
равна ![]() (или стремится к
(или стремится к ![]() ), интервал
называют точным (или асимптотически точным) доверительным
интервалом уровня доверия
), интервал
называют точным (или асимптотически точным) доверительным
интервалом уровня доверия ![]() .
.
Прежде чем рассматривать какие-то регулярные способы построения точных и асимптотических ДИ (доверительных интервалов), разберем два примера, предлагающих очень похожие способы. Далее мы попробуем извлечь из этих примеров некоторую общую философию построения точных и асимптотически точных доверительных интервалов. Начнем с нормального распределения как с наиболее важного и часто встречающегося.
Пусть ![]() ,
, ![]() ,
, ![]() — выборка объема
— выборка объема ![]() из нормального распределения
из нормального распределения ![]() , где
, где
![]() — неизвестный параметр, а
— неизвестный параметр, а ![]() известно.
Требуется построить точный ДИ для
параметра
известно.
Требуется построить точный ДИ для
параметра ![]() уровня доверия
уровня доверия ![]() .
.
Вспомним, что нормальное распределение устойчиво по суммированию: доказать бы!
Пусть ![]() имеет нормальное распределение
имеет нормальное распределение ![]() ,
, ![]() имеет нормальное распределение
имеет нормальное распределение ![]() , и эти случайные
величины независимы.
Тогда
, и эти случайные
величины независимы.
Тогда ![]() имеет нормальное распределение с параметрами
имеет нормальное распределение с параметрами
![]()
Поэтому
| случайная величина случайная величина случайная величина |
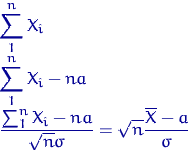 |
имеет распределение
|
Итак, величина ![]() имеет стандартное нормальное распределение.
имеет стандартное нормальное распределение.
По заданному ![]() найдем число
найдем число ![]() такое, что
такое, что
![]() . Число
. Число ![]() — квантиль уровня
— квантиль уровня
![]() стандартного нормального распределения:
стандартного нормального распределения:
![]()
или ![]() .
.
Напоминание:
Итак, ![]() , или
, или ![]() (квантили стандартного
нормального распределения).
(квантили стандартного
нормального распределения).
|
|
Разрешив неравенство ![]() относительно
относительно ![]() , получим точный
доверительный интервал
, получим точный
доверительный интервал
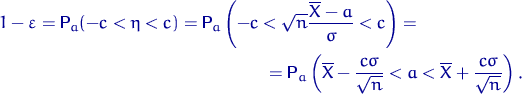
| (13) |
Можно подставить ![]() :
:
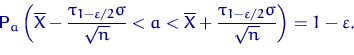
Итак, искомый точный доверительный интервал уровня доверия ![]() имеет вид
имеет вид
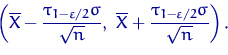
1. Зачем мы брали симметричные квантили? Почему не брать границы для
![]() вида
вида ![]() ?
Изобразить эти квантили на графике плотности. Как изменилось
расстояние между квантилями? Как изменится длина ДИ?
?
Изобразить эти квантили на графике плотности. Как изменилось
расстояние между квантилями? Как изменится длина ДИ?
2. Какой из двух ДИ одного уровня доверия и разной длины следует предпочесть?
3. Какова середина полученного в примере 23 ДИ? Какова его длина?
Что происходит с границами ДИ при ![]() ?
?
Пусть ![]() ,
, ![]() ,
, ![]() — выборка объема
— выборка объема ![]() из показательного распределения
из показательного распределения ![]() , где
, где
![]() . Требуется построить асимптотический (асимптотически точный)
ДИ для параметра
. Требуется построить асимптотический (асимптотически точный)
ДИ для параметра ![]() уровня доверия
уровня доверия ![]() .
.
Вспомним ЦПТ:
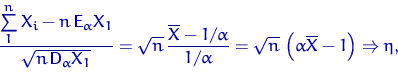
где случайная величина ![]() имеет стандартное нормальное распределение.
По определению слабой сходимости, при
имеет стандартное нормальное распределение.
По определению слабой сходимости, при ![]()
![]()
То есть
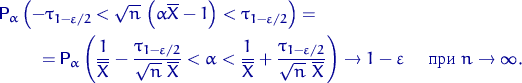
Итак, искомый асимптотический ДИ уровня доверия ![]() имеет вид
имеет вид
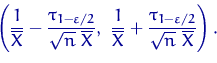
Сформулируем общий принцип построения точных ДИ:
![]()
Совершенно аналогично выглядит общий принцип построения асимптотических ДИ:
![]()
Часто в качестве ![]() и
и ![]() берут квантили
уровня
берут квантили
уровня ![]() и
и ![]() распределения
распределения ![]() .
Но, вообще говоря, квантили следует выбирать так, чтобы получить наиболее
короткий ДИ.
.
Но, вообще говоря, квантили следует выбирать так, чтобы получить наиболее
короткий ДИ.
Попробуем, пользуясь приведенной выше схемой, построить точный
доверительный интервал для параметра ![]() равномерного на
равномерного на ![]() распределения.
Мы знаем, что если
распределения.
Мы знаем, что если ![]() имеют распределение
имеют распределение ![]() , то
, то
![]() имеют распределение
имеют распределение ![]() . Тогда величина
. Тогда величина
![]()
распределена так же, как максимум из ![]() независимых равномерно
распределенных на
независимых равномерно
распределенных на ![]() случайных величин, то есть имеет не зависящую
от параметра
случайных величин, то есть имеет не зависящую
от параметра ![]() функцию распределения
функцию распределения
![\begin{displaymath}
F_{Y_{(n)}}(y)={\mathsf P}\,{\!}_\theta(\eta<y)=\begin{cases}
0, & y<0 \cr
y^n, & y\in[0,\,1] \cr
1, & y\gt 1.\end{cases}\end{displaymath}](img713.gif)
Для любых положительных ![]() и
и ![]()
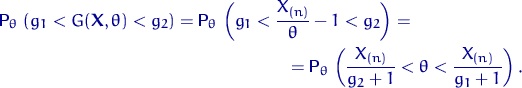
| (14) |
Длина доверительного интервала равна ![]() и уменьшается с ростом
и уменьшается с ростом ![]() и
и ![]() и с их сближением.
и с их сближением.
Плотность распределения ![]() на отрезке
на отрезке ![]() равна
равна ![]() и монотонно
возрастает. Поэтому самые большие значения квантилей
и монотонно
возрастает. Поэтому самые большие значения квантилей ![]() и
и ![]() при самом маленьком расстоянии между ними и
при фиксированной площади под графиком плотности достигается
выбором
при самом маленьком расстоянии между ними и
при фиксированной площади под графиком плотности достигается
выбором ![]() , а
, а ![]() такого, чтобы
такого, чтобы
![]() .
.
![]()
Подставим найденные квантили в (14):
![\begin{displaymath}
1-\varepsilon={\mathsf P}\,{\!}_\theta\left(\sqrt[n]{\vareps...
...}{2} < \theta < \frac{X_{(n)}}{1+\sqrt[n]{\varepsilon}}\right).\end{displaymath}](img721.gif)
Из упражнения видно, что функция ![]() вида
вида
![]() не годится для построения
точного ДИ для
не годится для построения
точного ДИ для ![]() при известном
при известном ![]() , а тем более при
неизвестном
, а тем более при
неизвестном ![]() . В следующей главе мы займемся поиском подходящих
функций. Следующий пример (как и пример 24) показывает, что ЦПТ
дает универсальный вид функции
. В следующей главе мы займемся поиском подходящих
функций. Следующий пример (как и пример 24) показывает, что ЦПТ
дает универсальный вид функции ![]() для построения асимптотических
ДИ.
для построения асимптотических
ДИ.
Пусть ![]() ,
, ![]() ,
, ![]() — выборка объема
— выборка объема ![]() из распределения Пуассона
из распределения Пуассона ![]() , где
, где
![]() . Требуется построить асимптотический
ДИ для параметра
. Требуется построить асимптотический
ДИ для параметра ![]() уровня доверия
уровня доверия ![]() .
Вспомним ЦПТ:
.
Вспомним ЦПТ:
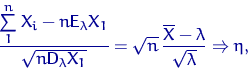
где ![]() имеет стандартное нормальное распределение.
По определению слабой сходимости, при
имеет стандартное нормальное распределение.
По определению слабой сходимости, при ![]()
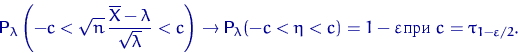
Но разрешить неравенство под знаком вероятности относительно ![]() не просто — получается квадратное неравенство из-за корня в знаменателе.
Не испортится ли сходимость, если мы заменим
на
не просто — получается квадратное неравенство из-за корня в знаменателе.
Не испортится ли сходимость, если мы заменим
на ![]() ?
?
По свойствам слабой сходимости, если ![]() и
и ![]() , то
, то ![]() .
Оценка
.
Оценка ![]() состоятельна, поэтому
состоятельна, поэтому
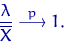
Тогда
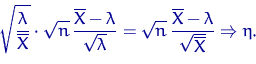
Поэтому и
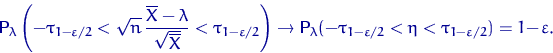
Разрешая неравенство под знаком вероятности относительно ![]() , получим
, получим
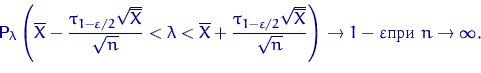
Итак, искомый асимптотический ДИ уровня доверия ![]() имеет вид
имеет вид
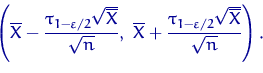
Вместо ЦПТ для построения асимптотических ДИ можно использовать
асимптотически нормальные оценки (что по сути — та же ЦПТ):
если ![]() — АНО для параметра
— АНО для параметра ![]() с коэффициентом
с коэффициентом
![]() , то
, то
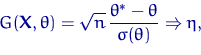
где ![]() имеет стандартное нормальное распределение.
имеет стандартное нормальное распределение.
Если ![]() в знаменателе мешает, то, как в примере 26,
ее можно заменить состоятельной оценкой
в знаменателе мешает, то, как в примере 26,
ее можно заменить состоятельной оценкой ![]() . Достаточно,
чтобы функция
. Достаточно,
чтобы функция ![]() была непрерывной во всей области
была непрерывной во всей области ![]() .
.
Требуется лишь ответить себе: почему ![]() — состоятельная оценка для
— состоятельная оценка для
![]() ?
?