Квантиль (она, моя, ж.р.)

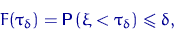
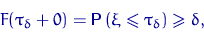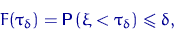
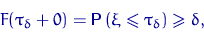Определение.  Число $\tau_\delta$ называется квантилью порядка (уровня) $\delta$ распределения $\mathscr F$ (с функцией распределения $F$), если
 $$  $$.

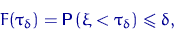
Замечание. Если чисел, удовлетворяющих  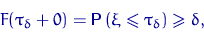$$  $$ несколько (целый интервал), то в качестве квантили берут или левую границу, или (чаще) середину этого интервала.


Впрочем, это уже от лукавого. В любом случае получается полный бред, если захотеть, скажем, найти квантиль уровня 1/3 распределения Бернулли с параметром 2/3. Никакого смысла в "квантилях" 0 или 1/2 (левая или средняя точка интервала от 0 до 1) обнаружить не удается. Впрочем, в самом желании найти квантиль уровня 1/3 распределения Бернулли с параметром 2/3 смысла не больше.

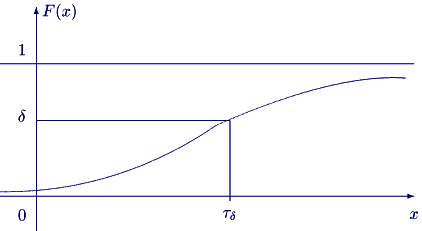
Никаких проблем не возникает в случае, когда функция распределения $F$ непрерывна и (главное) строго монотонна. Тогда квантиль $\tau_\delta$ порядка $\delta$ — единственное число, удовлетворяющее уравнению  $F(\tau_\delta)=\delta$

$$

В статистике определяют понятие выборочной квантили, как квантили того же порядка для выборочной (эмпирической) функции распределения.

Определение.  Число
$$

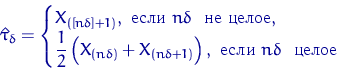
называется выборочной квантилью порядка (уровня) $\delta$ для выборки ${\mathbf X}=(X_1, \ldots, X_n)$.

Напомним также, что квантиль уровня 0.5 называется медианой распределения (выборочной медианой выборочного распределения).