next up previous index
Next:  Асимптотически нормальные оценки   Up:  Сравнение оценок   Previous:  Среднеквадратический подход

3.2.   Единственность эффективной оценки в классе с заданным смещением

Теорема 5.

Если $\theta^*_1\in K_b$ и $\theta^*_2\in K_b$ — две эффективные оценки в классе $K_b$, то с вероятностью 1 они совпадают: ${\mathsf P}_\theta\,(\theta^*_1=\theta^*_2)=1$.

Доказательство теоремы 5. Заметим сначала, что ${\mathsf E}_\theta\,(\theta^*_1-\theta)^2={\mathsf E}_\theta\,(\theta^*_2-\theta)^2$. Действительно, так как $\theta^*_1$ эффективна в классе $K_b$, то она не хуже оценки $\theta^*_2$, то есть

\begin{displaymath} {\mathsf E}_\theta\,(\theta^*_1-\theta)^2 \leqslant {\mathsf E}_\theta\,(\theta^*_2-\theta)^2,\end{displaymath}

и наоборот. Поэтому ${\mathsf E}_\theta\,(\theta^*_1-\theta)^2={\mathsf E}_\theta\,(\theta^*_2-\theta)^2$.

Рассмотрим оценку $\theta^*=\dfrac{\theta^*_1+\theta^*_2}{2}$. Она также принадлежит классу $K_b$. доказать!

Вычислим ее среднеквадратическое отклонение. Заметим, что

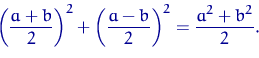\begin{equation} \left(\dfrac{a+b}{2}\right)^2+\left(\dfrac{a-b}{2}\right)^2= \dfrac{a^2+b^2}{2}.\end{equation}(6)

Положим $a=\theta^*_1-\theta$, $b=\theta^*_2-\theta$. Тогда $(a+b)/2=\theta^*-\theta$, $a-b=\theta^*_1-\theta^*_2$. Подставим эти выражения в (6) и возьмем математические ожидания обеих частей:

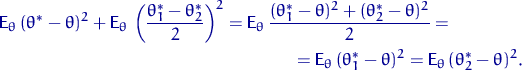
\begin{multline} {\mathsf E}_\theta\,(\theta^*-\theta)^2+{\mathsf E}_\theta\,\le... ...\,(\theta^*_1-\theta)^2={\mathsf E}_\theta\,(\theta^*_2-\theta)^2.\end{multline} (7)

Но оценка $\theta^*$ принадлежит $K_b$, то есть она не лучше, например, эффективной оценки $\theta^*_1$. Поэтому

\begin{displaymath} {\mathsf E}_\theta\,(\theta^*-\theta)^2 \geqslant {\mathsf E}_\theta\,(\theta^*_1-\theta)^2.\end{displaymath}

Сравнивая это неравенство с равенством (7), видим, что

\begin{displaymath} {\mathsf E}_\theta\,\left(\dfrac{\theta^*_1-\theta^*_2}{2}\r... ...овательно, } {\mathsf E}_\theta\,(\theta^*_1-\theta^*_2)^2 = 0.\end{displaymath}

Тогда почему? ${\mathsf P}_\theta\,(\theta^*_1=\theta^*_2)=1$, что и требовалось доказать.

Q.D.E.


Для примера рассмотрим сравнение двух оценок. Разумеется, сравнивая оценки попарно между собой, наилучшей оценки в целом классе не найти, но выбрать лучшую из двух тоже полезно. А способами поиска наилучшей в целом классе мы тоже скоро займемся.

Пример 11.

Пусть $X_1$, $\ldots$, $X_n$ — выборка объема $n$ из равномерного распределения ${\mathsf U}_{0,\theta}$, где $\theta\gt$. В примерах 4 и 9 мы нашли ОМП $\hat\theta=X_{(n)}$ и ОММ по первому моменту $\theta^*=2\overline X$. Сравним их в среднеквадратичном.

Оценка $\theta^*=2\overline X$ несмещенная, поэтому

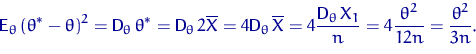
\begin{displaymath} {\mathsf E}_\theta\,(\theta^*-\theta)^2={\mathsf D}_\theta\,... ...eta\, X_1}{n}= 4 \dfrac{\theta^2}{12 n}= \dfrac{\theta^2}{3 n}.\end{displaymath}

Для $\hat\theta=X_{(n)}$ имеем

\begin{displaymath} {\mathsf E}_\theta\,(\hat\theta-\theta)^2={\mathsf E}_\theta\,\hat\theta^2 - 2\theta{\mathsf E}_\theta\, \hat\theta +\theta^2.\end{displaymath}

Посчитаем первый и второй момент случайной величины $\hat\theta=X_{(n)}$. Найдем (полезно вспомнить, как это делалось в прошлом семестре!) функцию распределения и плотность $\hat\theta$:

\begin{displaymath} {\mathsf P}_\theta\,(X_{(n)}<y)={\mathsf P}_\theta\,(X_1<y)^... ...{\theta^n}, & y\in[0,\theta], \cr 1, & y\gt\theta,\end{cases} \end{displaymath}

\begin{displaymath} f_{X_{(n)}}(y)= \begin{cases} 0, & \textrm{если } y\not\in[... ...y^{n-1}}{\theta^n}, & \textrm{если } y\in[0,\theta].\end{cases}\end{displaymath}

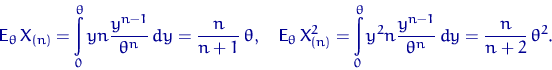
\begin{displaymath} {\mathsf E}_\theta\, X_{(n)}=\int\limits_0^\theta y n\dfrac{... ...a y^2 n\dfrac{y^{n-1}}{\theta^n}\,dy= \dfrac{n}{n+2}\,\theta^2.\end{displaymath}

Поэтому

\begin{displaymath} {\mathsf E}_\theta\,(X_{(n)}-\theta)^2=\dfrac{n}{n+2}\,\thet... ...ac{n}{n+1}\,\theta^2+ \theta^2=\dfrac{2}{(n+1)(n+2)}\,\theta^2.\end{displaymath}

При $n$=1, 2 квадратические отклонения равны, а при $n\gt 2$

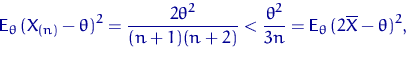
\begin{displaymath} {\mathsf E}_\theta\,(X_{(n)}-\theta)^2=\dfrac{2\theta^2}{(n+... ...ac{\theta^2}{3 n} ={\mathsf E}_\theta\,(2\overline X-\theta)^2,\end{displaymath}

то есть $X_{(n)}$ лучше, чем $2\overline X$. При этом ${\mathsf E}_\theta\,(X_{(n)}-\theta)^2$ стремится к нулю со скоростью $n^{-2}$, тогда как ${\mathsf E}_\theta\,(2\overline X-\theta)^2$ — со скоростью $n^{-1}$.

Упражнение.

1. Доказать, что $X_{(n)}\in K_b$, где $b(\theta)=-\dfrac{\theta}{n+1}$.

2. Доказать, что $\dfrac{n+1}{n} X_{(n)}\in K_0$ (несмещенная).

3. Сравнить оценки $\dfrac{n+1}{n} X_{(n)}$ и $X_{(n)}$ в среднеквадратичном.


N.I.Chernova
9 сентября 2002